
Viking Jupiter
I movimenti oscillatori delle navi: il mare ondoso
Dopo aver parlato dei moti oscillatori in questa quarta e ultima parte sarà sviluppata l’azione eccitatrice del mare ondoso. Con mare ondoso regolare s’intende un qualsiasi stato del mare che sia caratterizzato da onde tutte uguali tra loro, aventi la stessa direzione di propagazione. Secondo la teoria di Gestner, il periodo, cioè il tempo che intercorre fra il passaggio di due creste successive, è pari a :
\(T_0 = \sqrt {{2 \cdot π \cdot L_0} \over g}\)
dove
\(L_0\) = lunghezza dell’onda, cioè la distanza fra due creste successive
\(g\) = accelerazione di gravità.
La velocità di propagazione o celerità è
\(C = \sqrt {{g \cdot L_0} \over {2 \cdot π}}\)
L’azione eccitatrice dell’onda sulla nave è causata dall’impatto dell’onda sullo scafo. Il tempo che intercorre tra due impatti successivi \(T_i\) è denominato “periodo d’incontro”. Se la nave è ferma all’ancora in mare ondoso si ha \(T_i = T_0\) . Se la nave avanza con velocità \(V_n\) in una direzione obliqua con un angolo \(α\) rispetto alla direzione di propagazione delle onde si ha
\(T_i = {{L_0} \over {C - V_n \cdot cosα }} \)
Se avviene che il periodo d’incontro, o di eccitazione, coincida con un periodo \(T_n\) di oscillazione naturale della nave, si ha risonanza per quel particolare tipo di oscillazione con esaltazione delle escursioni massime e delle relative accelerazioni. Se la nave avanza con velocità \(V_n\) di verso contrario a quello delle onde, e tale, che il valore di \(T_i\) si riduca molto fino ad avvicinarsi al periodo completo di beccheggio \(T_l\), si ha la condizione di risonanza. In questa condizione avviene che la nave compie ampie oscillazioni longitudinali, che la fanno urtare contro le onde con violenza. In questa condizione è importate, per ridurre l’entità degli urti, che la parte inferiore della prora non emerga durante le oscillazioni. La maggiore distanza della prora dall’asse di rotazione comporta movimenti più ampi, e quindi maggiori tormenti dovuti alla forza d’inerzia. Per questo motivo, non conviene mettere grandi pesi a prora per non aumentare il momento d’inerzia di massa longitudinale, che incide direttamente sul periodo di oscillazione. Perciò se si verificasse il sincronismo fra \(T_i\) e \(T_l\) , il comandante della nave varierà opportunamente la velocità e la rotta.
I periodi di sussulto e di beccheggio, di solito, non differiscono molto l’uno dall’altro, e pertanto, in caso di risonanza, si possono determinare notevoli accelerazioni verticali, specialmente nelle zone prodiere.
Se una nave, con un’altezza metacentrica trasversale \((r-a)\) molto alta e quindi durissima con forti accelerazioni trasversali, avesse periodi di rollio e di beccheggio quasi uguali tra loro, con un periodo \(T_i\) d’incontro intermedio fra i due e con mare non perfettamente al traverso, si genererebbero oscillazioni trasversali e longitudinali. La prora urterebbe violentemente il mare con un’inclinazione trasversale, si verificherebbe un’eccentricità della reazione d’urto rispetto al piano di simmetria e quindi sollecitazione di torsione dello scafo e difficoltà a mantenere la rotta. In tutti questi fenomeni è da considerare l’azione indotta dello smorzamento causato dal mare. Il suo effetto è sempre quello di ridurre la velocità e l’ampiezza delle oscillazioni, per cui diventa un importante fattore a favore della sicurezza, specialmente in caso di risonanza.
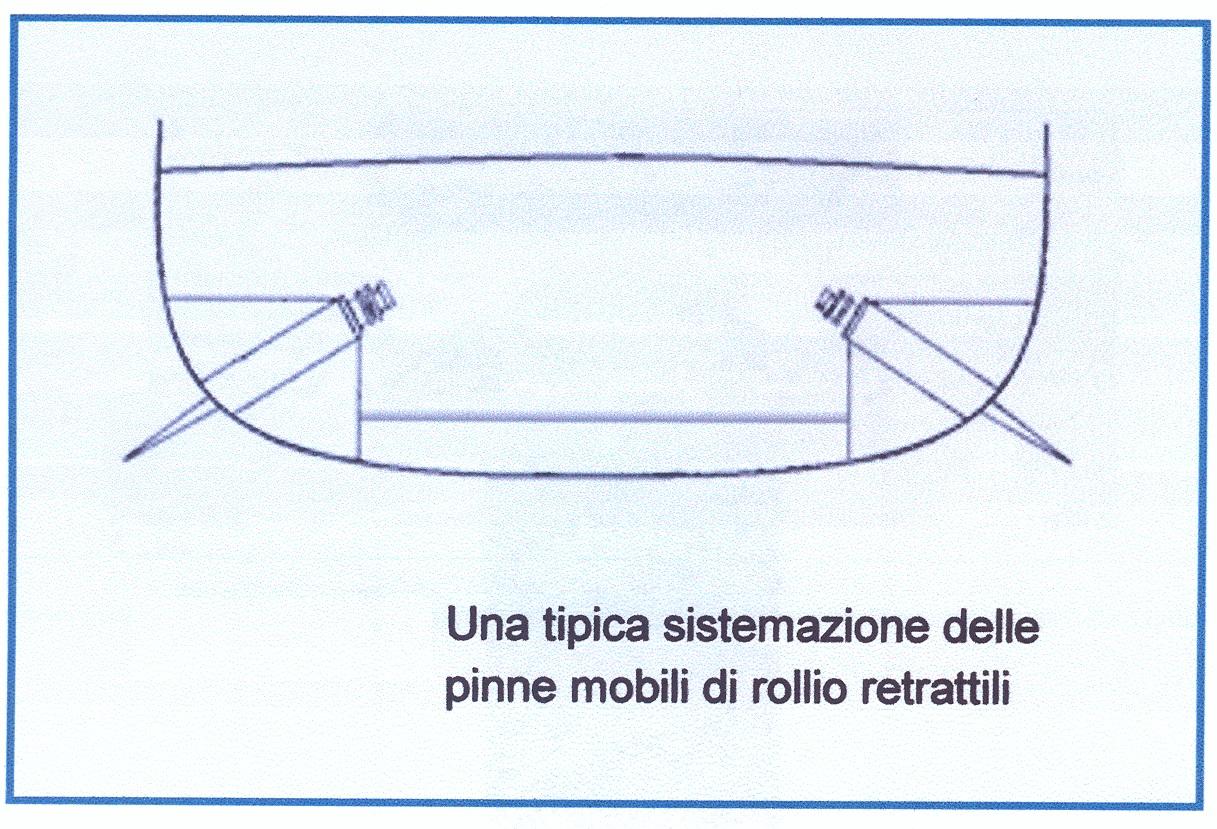
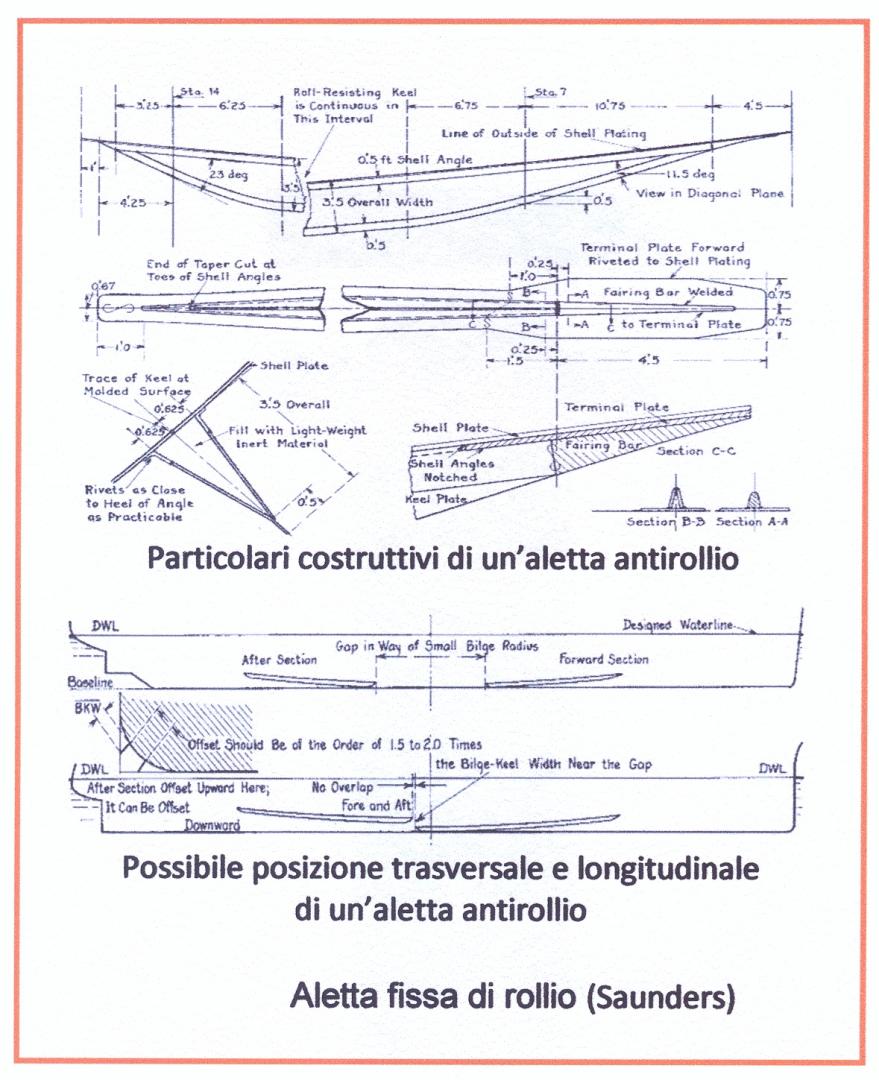
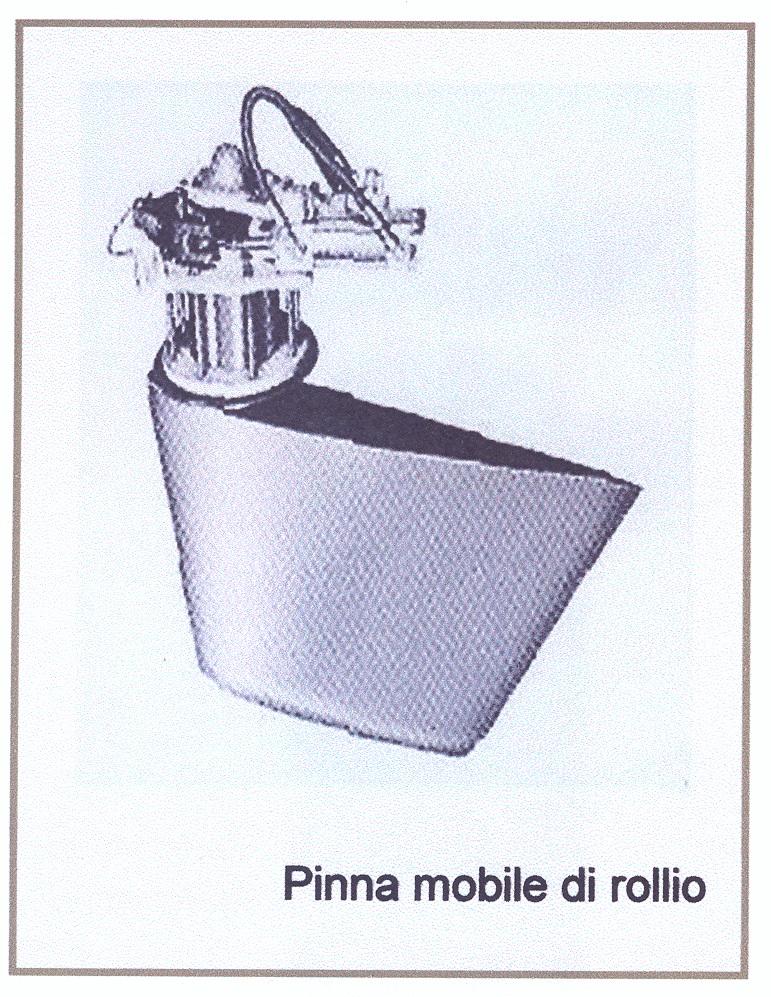
Le alette di rollio (Figura 8), che si estendono per una notevole lunghezza, e le pinne mobili (Figura 9), che possono essere anche retrattili (Figura 13), migliorano notevolmente la capacità della nave di smorzamento delle oscillazioni trasversali, specialmente se la carena ha la sezione maestra a semicerchio (Figura 10). Le pinne esercitano una notevole azione con nave in moto, e poca con nave ferma; il contrario vale per le alette.
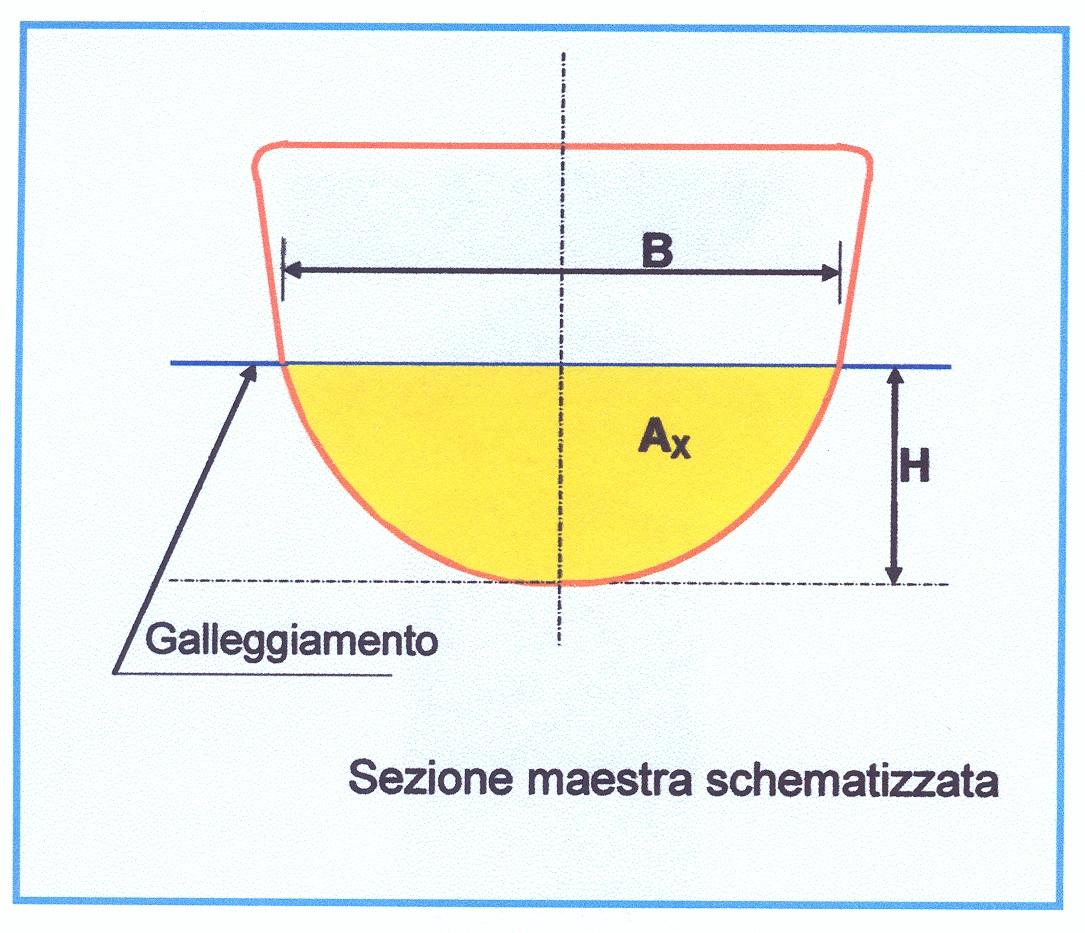
La forma di carena, in particolare il coefficiente di finezza della sezione maestra \(C_x\) , ha una forte influenza sull’entità dello smorzamento del rollio.
Infatti, poiché
\(C_x = {A_x \over {B \cdot H}}\)
dove
\(A_x\) = area della sezione maestra immersa
\(B\) = larghezza al galleggiamento
\(H\) = immersione
1) se è un valore piccolo si ha un’area della sezione maestra immersa piccola per arrivare al limite di una sezione triangolare (Figura 11); in questo caso la chiglia ha effetto di aletta di rollio;
2) se è un valore medio, si ha un’area della sezione maestra immersa tale da rappresentare una forma ad U (Figura 10);
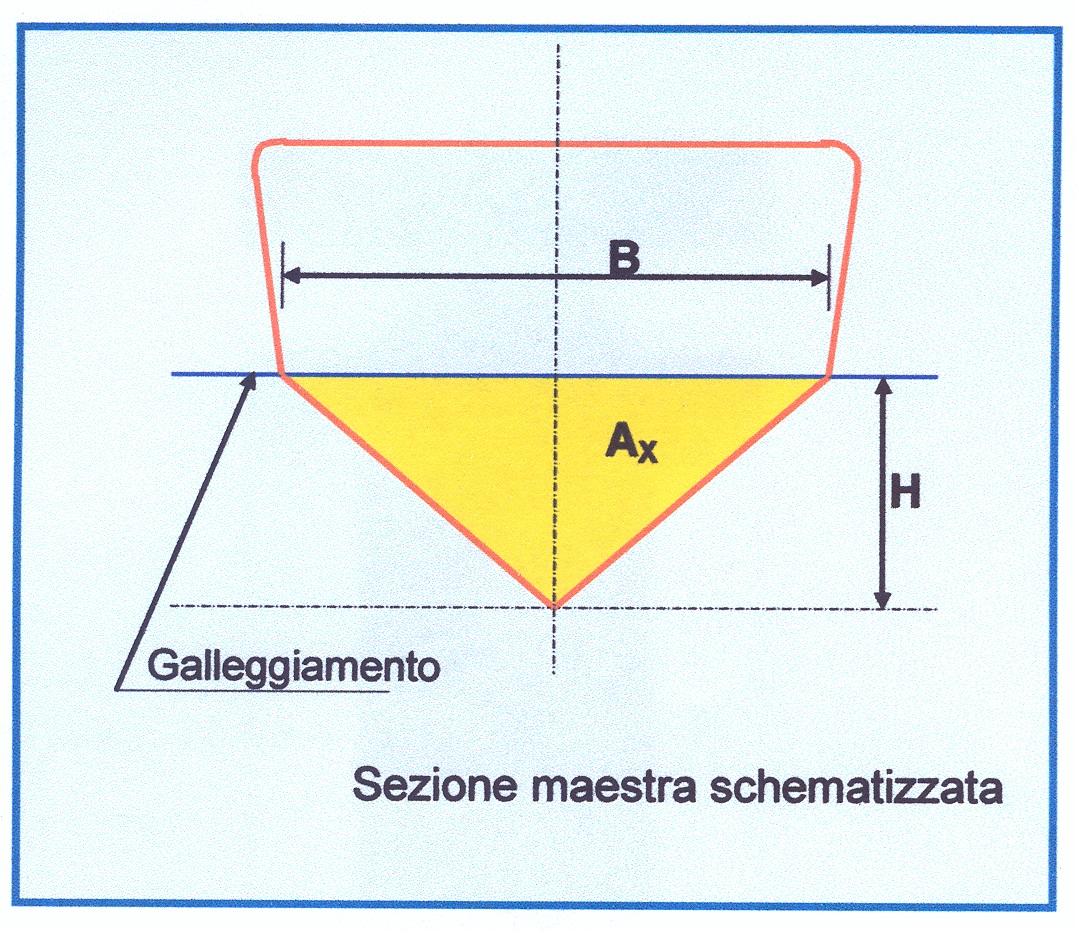
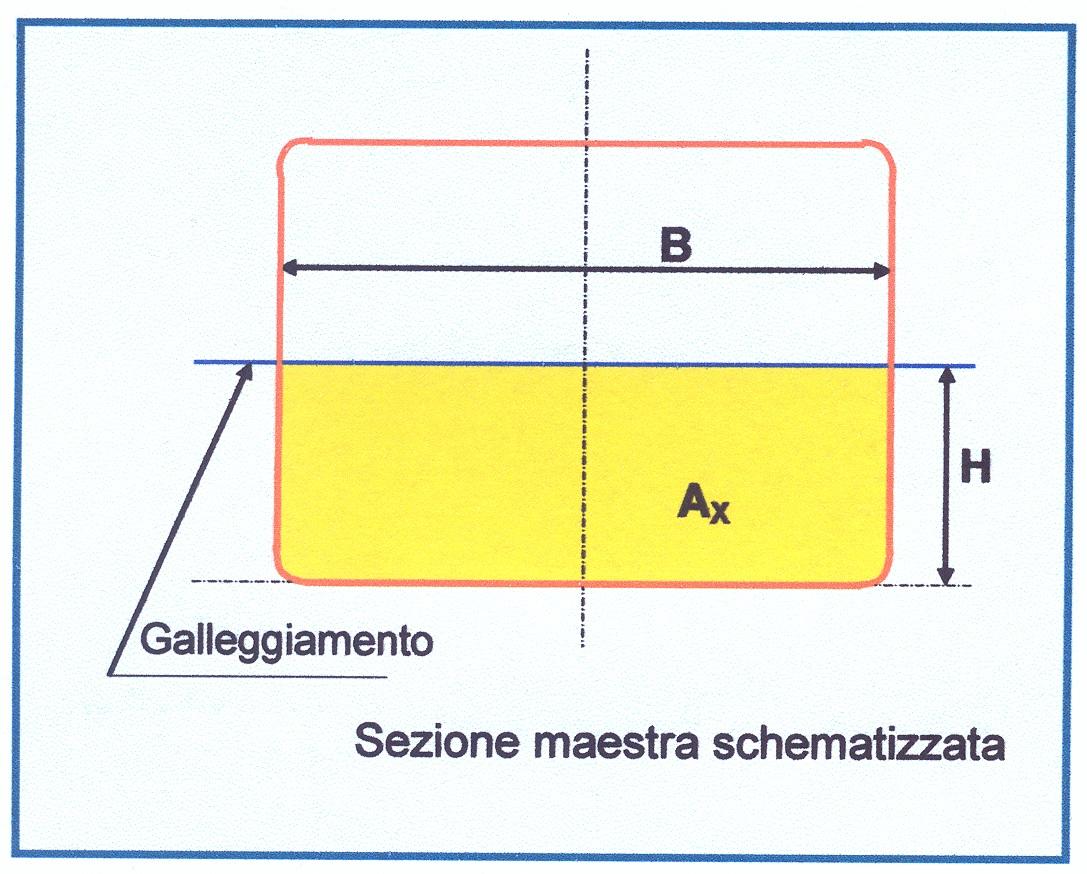
3) se è un valore grande, si ha un’area della sezione maestra immersa tale da coprire quasi tutta la superficie del rettangolo formato dalla larghezza \(B\) e dall’immersione \(H\) (Figura 12); anche in questo caso il ginocchio ha l’effetto di aletta di rollio.
Infine possiamo affermare che una nave in movimento, con mare al traverso, avrà sempre minore angolo di rollio di quello che avrebbe se fosse ferma, perché il coefficiente di smorzamento aumenta all’aumentare della velocità, e che l’angolo massimo di beccheggio in mare tempestoso sarà comunque inferiore a quello con mare regolare, in condizioni di risonanza, perché i fenomeni di risonanza avvengono in misura molto meno pronunciata che con onde regolari.
Angelo Sinisi
©PressMare - riproduzione riservata





