
La Nave scuola Palinuro (© Marina Militare)
La stabilità delle navi: stabilità dinamica
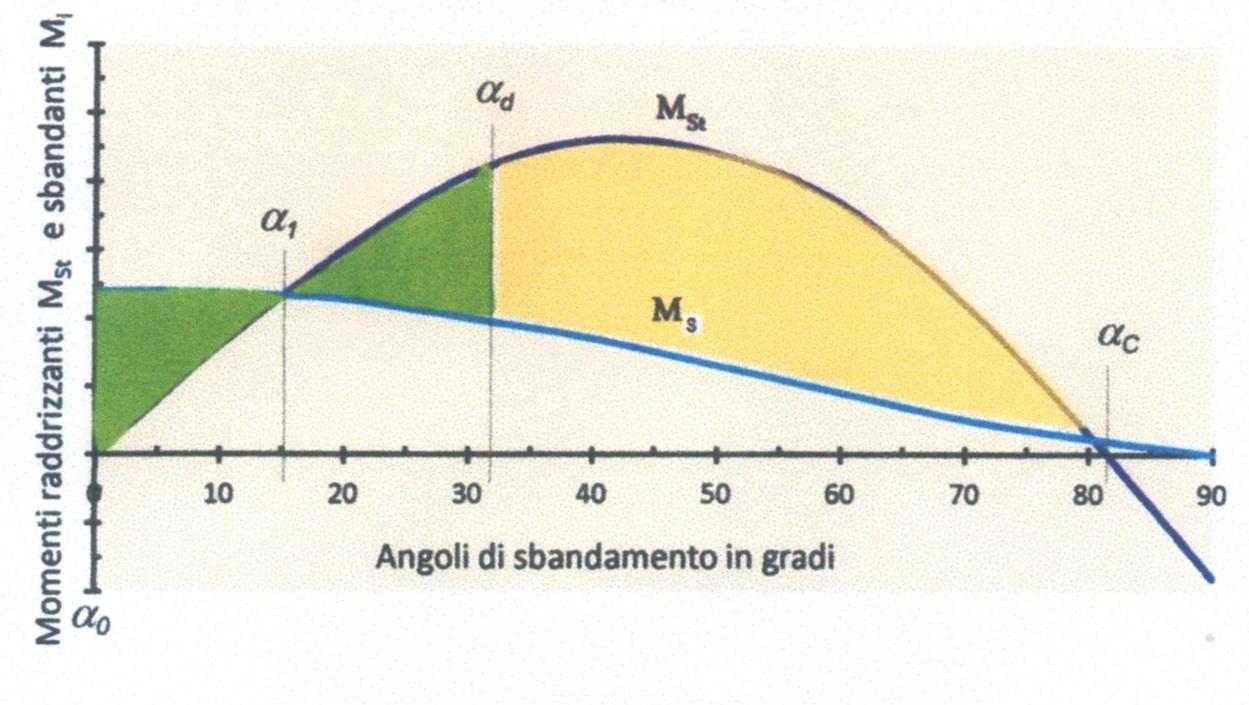
In questa quarta ed ultima parte dell’articolo parlerò della stabilità dinamica delle navi. Nel diagramma rappresentato nella Figura 14 , che è tipico per le navi inizialmente stabili, abbiamo solo due angoli di momento nullo: l’angolo \(∝ = 0\) di equilibrio stabile e l’angolo \(∝ = ∝_C\) di equilibrio instabile.
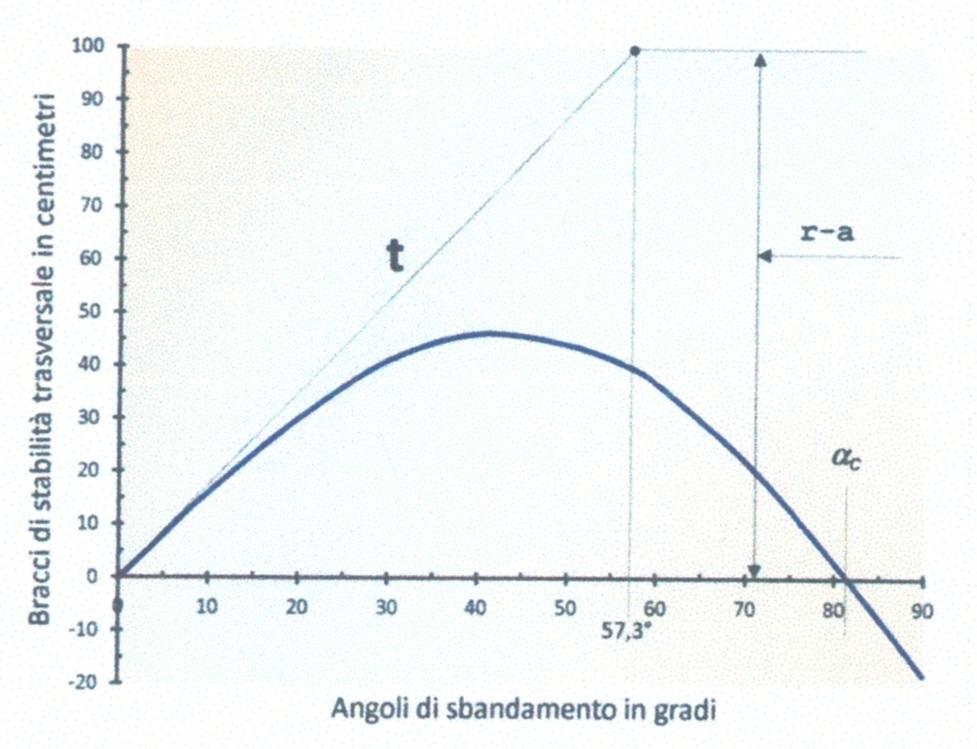
Se la forza inclinante è tale da abbattere trasversalmente la nave di un angolo \(∝< ∝_C \), la nave riprende la posizione iniziale al cessare della forza. Se, invece, l’angolo diventa \(∝>∝_C \), la nave non riprende la posizione iniziale al cessare della forza inclinante, perché come nelle Figura 11 e Figura 12c il momento raddrizzante o di stabilità hanno lo stesso verso della forza sbandante.
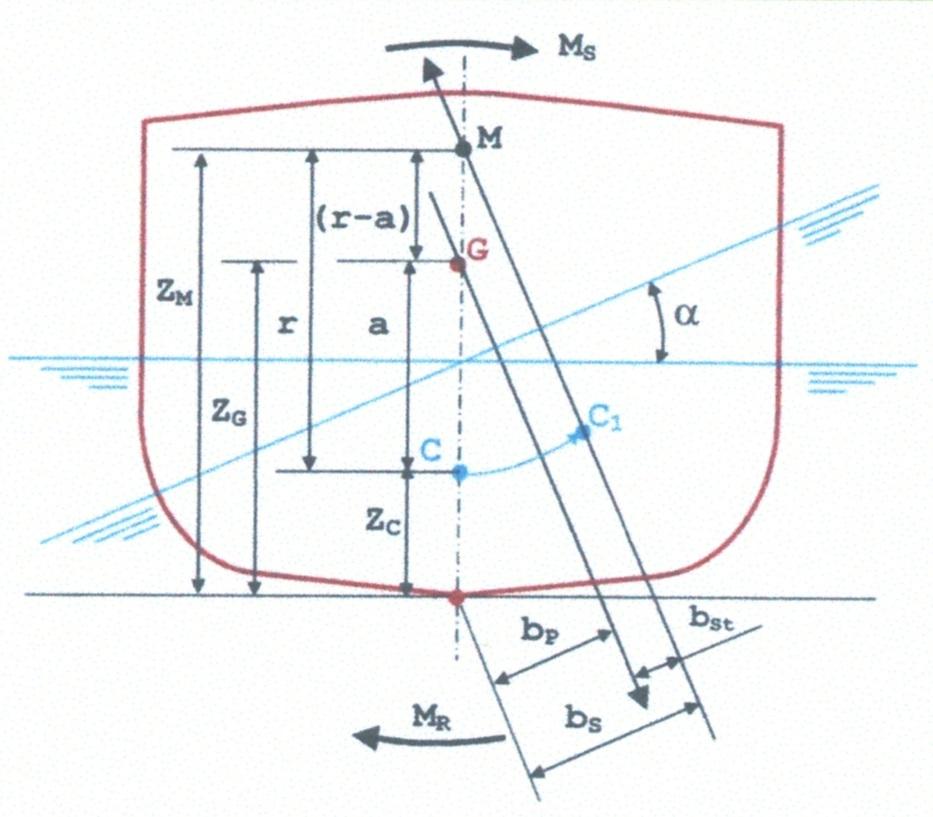
Gli elementi necessari per costruire il diagramma di stabilità per ogni dislocamento fissato \(∆\) sono i bracci di stabilità trasversale \(b_{St}\) (Figura 18), dedotti dai grafici delle carene inclinate, da cui si ricavano alle varie inclinazioni \(∝\) i bracci della spinta, dai quali, secondo la posizione del centro di gravità \(G\) si detraggono i bracci del peso \(b_p\), relativo al dislocamento \(∆\).
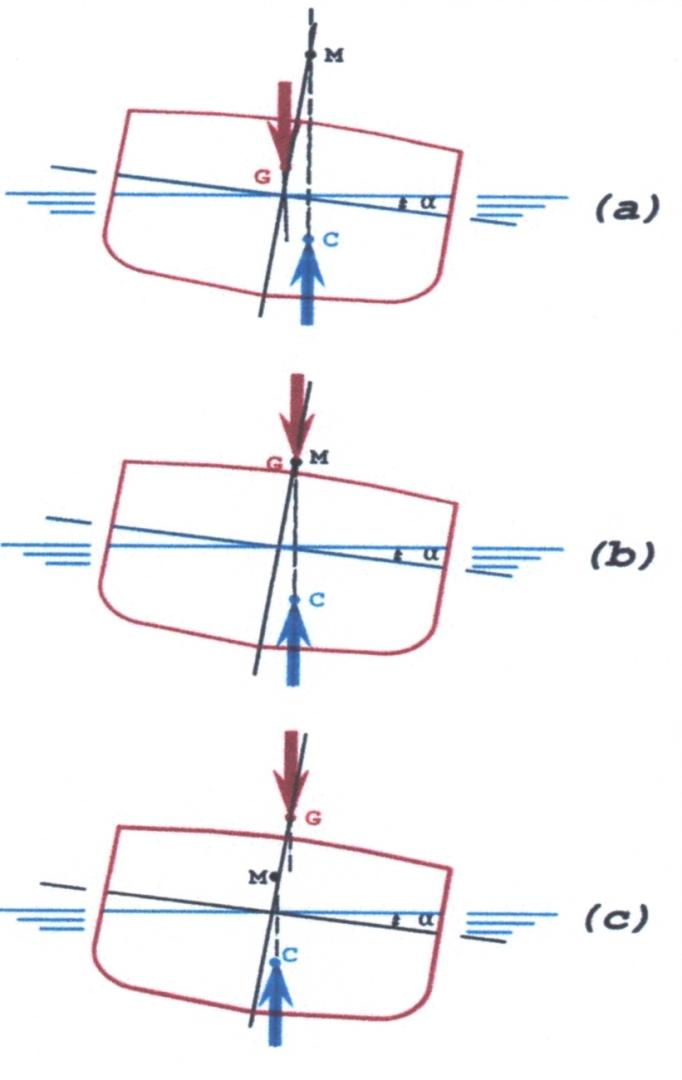
Durante i calcoli dei bracci di stabilita, con l’aumentare dell’angolo di abbattimento \(∝\), i piani di galleggiamento tagliano la coperta e di conseguenza la sovrastruttura. Ovviamente si terrà conto dell’una e dell’altra solo se sono stagne. Si chiama stabilità dinamica il lavoro che occorre per portare la nave all’inclinazione trasversale \(∝\). Se indichiamo con \(L\) questo lavoro si ha
\(L=∫_0^∝{M_{St} {d ∝}}\)
Quindi, il diagramma di stabilità dinamica si ottiene integrando il diagramma dei momenti di stabilità \(M_{St}\). Il valore di \(Lc\) della curva \(L\) (Figura 16) , che è il lavoro che occorre per portare la nave all’angolo di capovolgimento \(∝_C\), è la “riserva totale di stabilità”, cioè l’energia che ha la nave ad opporsi alla forza sbandante \(F_i\) (Figura 11). Il “momento inclinante” \(M_S\) (Figura 18) è il momento generato da quelle forze che modificano la posizione iniziale della nave. Queste forze, che generano il momento inclinante, possono essere causate dallo spostamento di un peso a bordo, dal vento, dal mare ondoso, dall’azione del timone, ecc..
La forma della curva o del diagramma del momento inclinante cambia secondo la causa che lo realizza. Supponiamo di applicare ad una nave, avente per momento di stabilità \(M_{St}\) , un momento sbandante \(M_S\) (Figura 17). La nave dalla posizione \(∝_0\) iniziale si abbatte trasversalmente, raggiungendo l’angolo \(∝_1\), lo sorpassa, a causa della forza d’inerzia, e raggiunge l’angolo \(∝_d\). Il momento raddrizzante si oppone, per cui la nave torna indietro, sorpassa l’angolo \(∝_1\) e, avendo perso parte della forza d’inerzia, non raggiunge l’angolo \(∝_0\) \((∝=0)\). Quindi torna ad inclinarsi dalla parte opposta, raggiunge l’angolo \(∝_1\) , e lo sorpassa.
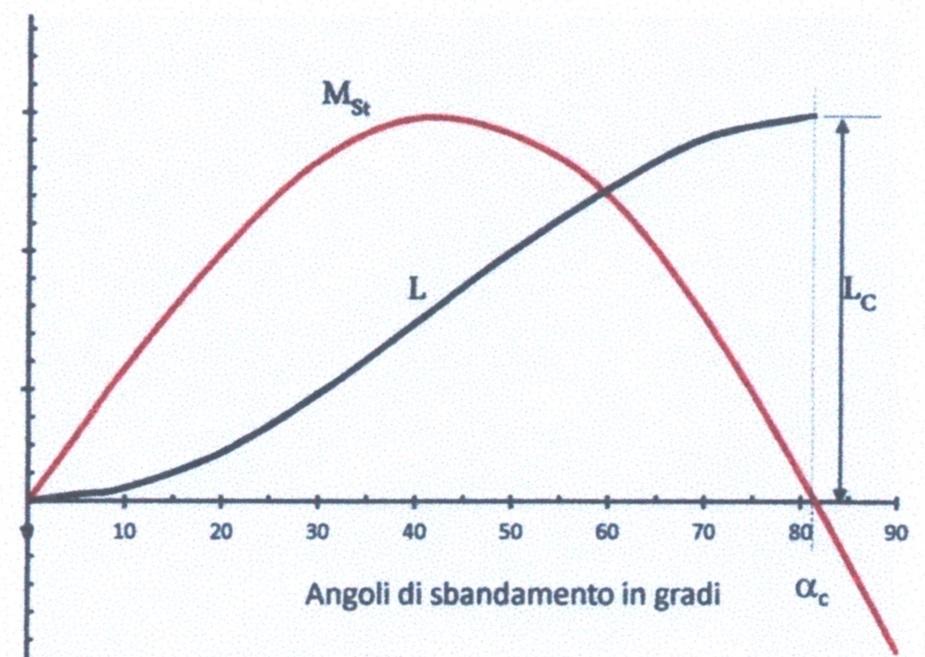
A causa della forza d’inerzia, che dopo ogni inclinazione diventa sempre minore, la nave compie una serie di oscillazioni ed esaurita la forza d’inerzia, resta inclinata dell’angolo \(∝_1\) , dove \(M_{S}=M_{St}\) . L’angolo \(∝_1\) se è inferiore a 15 gradi si chiama “angolo d’ingavonamento”, se è superiore a 15 gradi si chiama “angolo di abbattimento”, mentre l’angolo \(∝_d\) si chiama angolo di equilibrio dinamico (Figura 17). Esso è tale per cui le aree verdi a sinistra e a destra dell’angolo \(∝_1\) sono uguali e resta a destra dell’angolo \(∝_d\) un’area (gialla) (Figura 17) che corrisponde all’energia di riserva che il momento raddrizzante ha per riportare, in sicurezza, la nave nella posizione relativa all’angolo \(∝_1\). Se l’area verde a sinistra dell’angolo \(∝_1\) fosse maggiore dell’area verde a destra dell’angolo \(∝_1\) vuol dire che l’energia (o lavoro) prodotta dal momento inclinante è superiore all’energia prodotta dal momento stabilizzante (l’area gialla verrebbe a mancare nella Figura 17) e la nave si rovescerebbe. Per cui con certezza possiamo affermare che è enormemente importante la posizione dell’angolo di equilibrio dinamico \(∝_d\) .
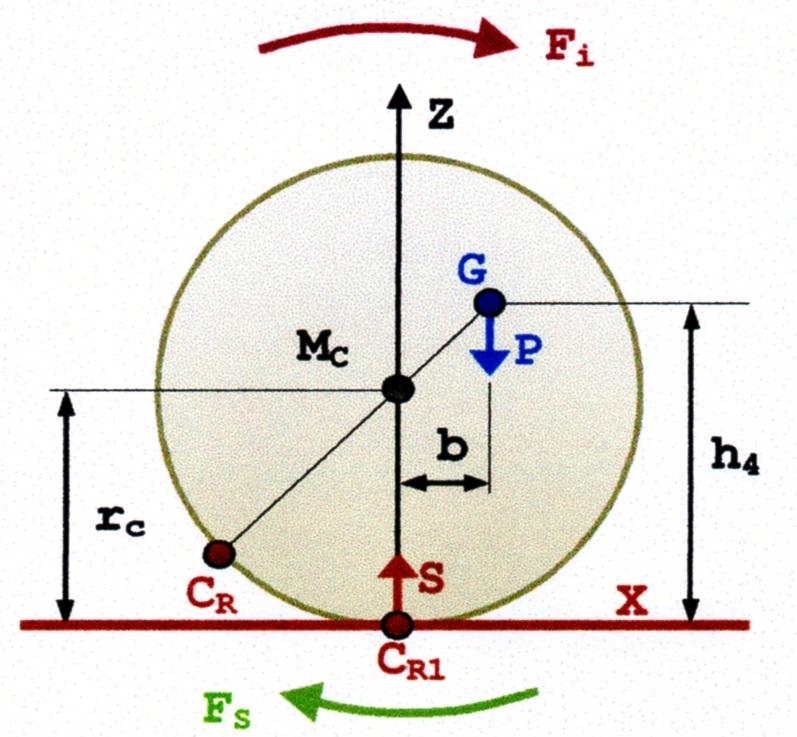
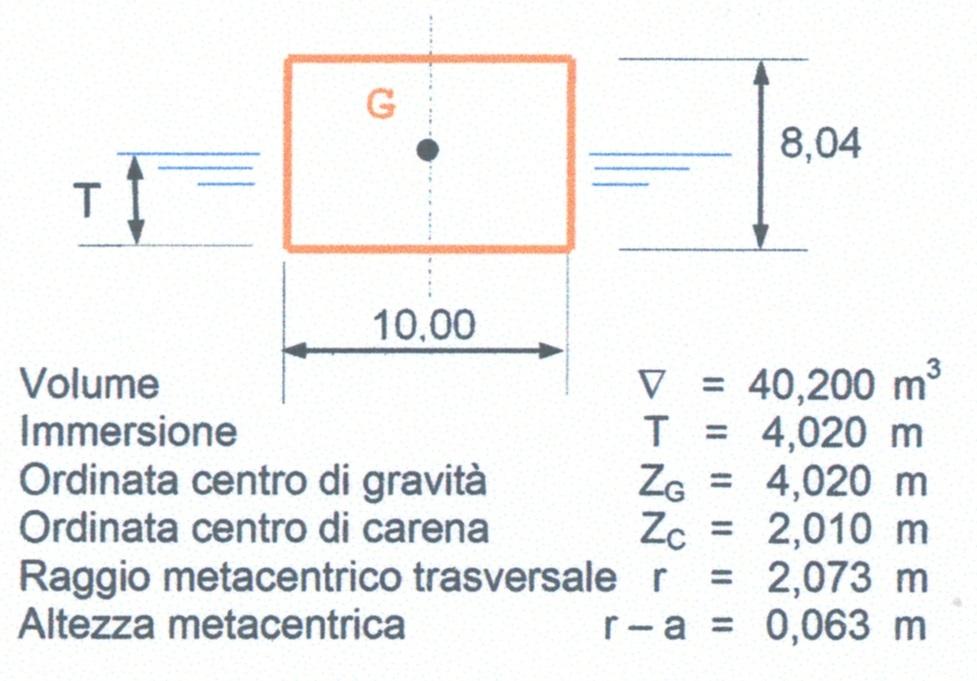
Da quanto detto si evidenzia che la stabilità è sicuramente influenzata dalla posizione baricentrica e dalla larghezza. Ma tra i due chi ha maggiore efficacia è la larghezza. Infatti se consideriamo due prismi di lunghezza unitaria come quelli della Figura 19 e della Figura 20 avremo che il prisma della Figura 19 poiché \((r-a)>0\) vuol dire che è in equilibrio stabile, ma, avendo un valore leggermente superiore allo zero, non ha un momento raddrizzante sufficiente per opporsi anche ad una piccola forza sbandante. Cioè se una simile condizione di stabilità l’avesse una nave sarebbe disastroso, perché, come precedentemente detto, alla prima ondata la nave si capovolgerebbe.
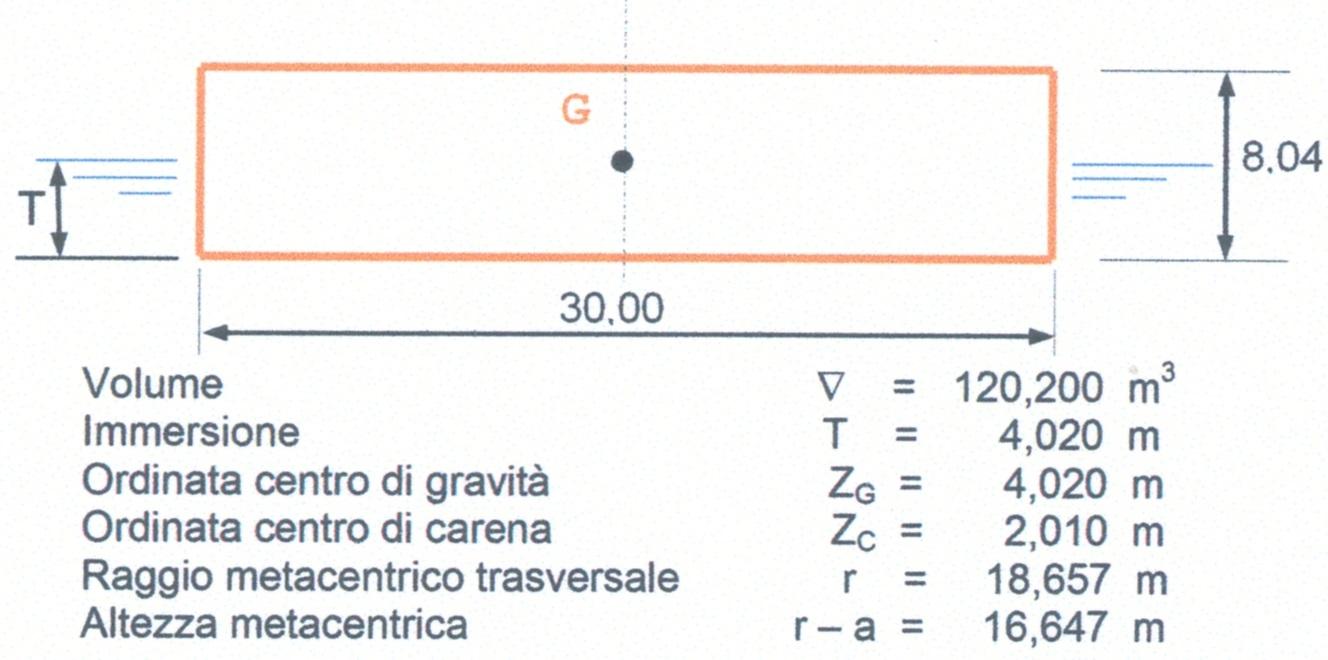
Al contrario, il prisma della Figura 20 , avendo una larghezza tre volte maggiore dell’altro, ha un raggio metacentrico 9 volte superiore. Cioè il raggio metacentrico varia con il quadrato del rapporto tra le larghezze, avendo la stessa immersione.
Tuttavia un’altezza metacentrica \((r - a = 16,647 m)\) come quella del prisma della Figura 20 è elevata e perciò dannosa. Infatti un’altezza metacentrica elevata renderebbe fastidiosa la vita di bordo durante la navigazione. Questo avviene in quanto il periodo di oscillazione \(T\) della nave è legato all’altezza metacentrica trasversale dalla relazione \(T=K⁄\sqrt{r-a}\) con \(K\) variabile a seconda del tipo di nave. Si deduce che con un valore di \((r-a)\) elevato si ha un momento raddrizzante molto alto per cui si abbassa il periodo di oscillazione con forti accelerazioni di gravità e la nave acquista in mare ondoso un comportamento di nave definita “troppo dura”.
Al contrario una nave con un valore di \((r-a)\) basso ha un momento raddrizzante basso per cui, con mare mosso, si avranno delle oscillazioni molto lente ma molto ampie tali che, in casi estremi, sono cause di capovolgimenti. Un altro elemento importante che influisce sul periodo di rollio \(T\) della nave è incluso nel coefficiente \(K\) ed è il “momento d’inerzia di massa” del sistema “nave-acqua” rispetto all’asse baricentrico di rotazione. Ovviamente il suo effetto può essere positivo o negativo come se indirettamente agisse sul valore dell’altezza metacentrica \((r-a)\). Per affrontare questo problema entreremmo in argomentazioni lunghe e complesse e lo spazio e il tempo non lo consentono.
Anche negli scafi plananti l’altezza metacentrica \((r-a)\) ha una enorme importanza perché condiziona anche la stabilità dinamica in corsa. Infatti, nelle imbarcazioni strette e/o molto alte e veloci, in virata, si verifica che il bordo della coperta si avvicina paurosamente al livello del mare.
Quindi per avere un buon comportamento in mare, relativamente al rollio, ripeto le parole della prima frase dell’articolo: la stabilità trasversale va ricercata attraverso corrette proporzioni di scafo.
Angelo Sinisi
©PressMare - riproduzione riservata





