
La carena a spigolo o planante - quinta parte
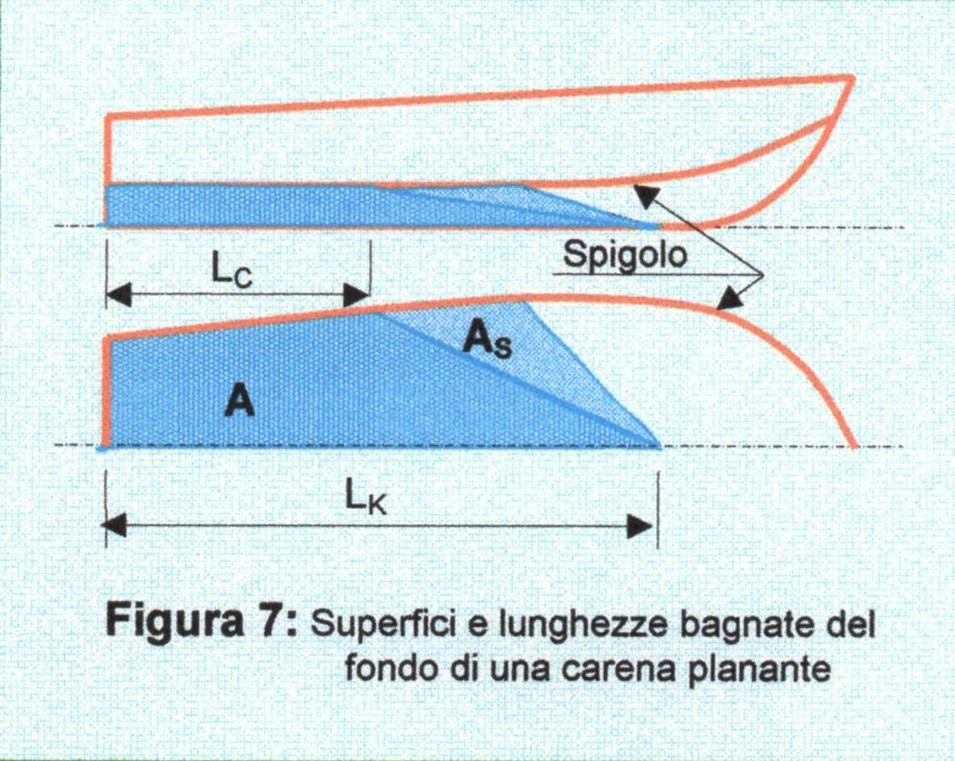
Nelle pareti precedenti abbiamo trovato tutti gli elementi per calcolare, alle varie velocità e relativi assetti dello scafo in planata, la superficie bagnata di carena
\(A=(\lambda \cdot B_C^2)/cos \beta\)
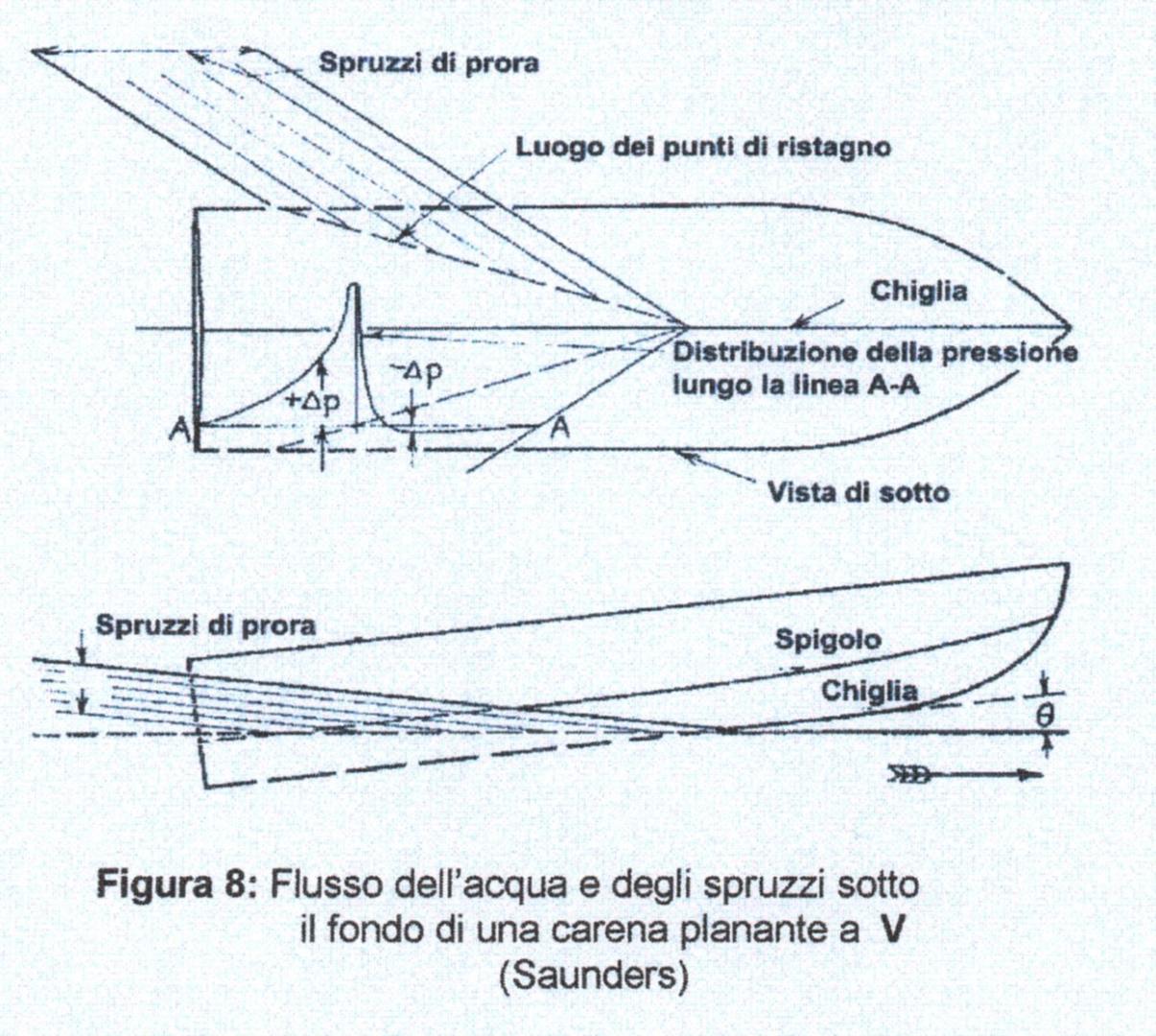
Per il calcolo della resistenza di attrito non è sufficiente la suddetta superficie, perché essendoci un alta quantità di spruzzi sarà necessario calcolare la superficie bagnata dagli spruzzi \(A_S\) e sommarla alla superficie \(A\) (Figure 7 e 8). L’equazione che trova la superficie bagnata dagli spruzzi è
\(A_S =(\Delta \lambda \cdot B_C^2)/cos \beta\)
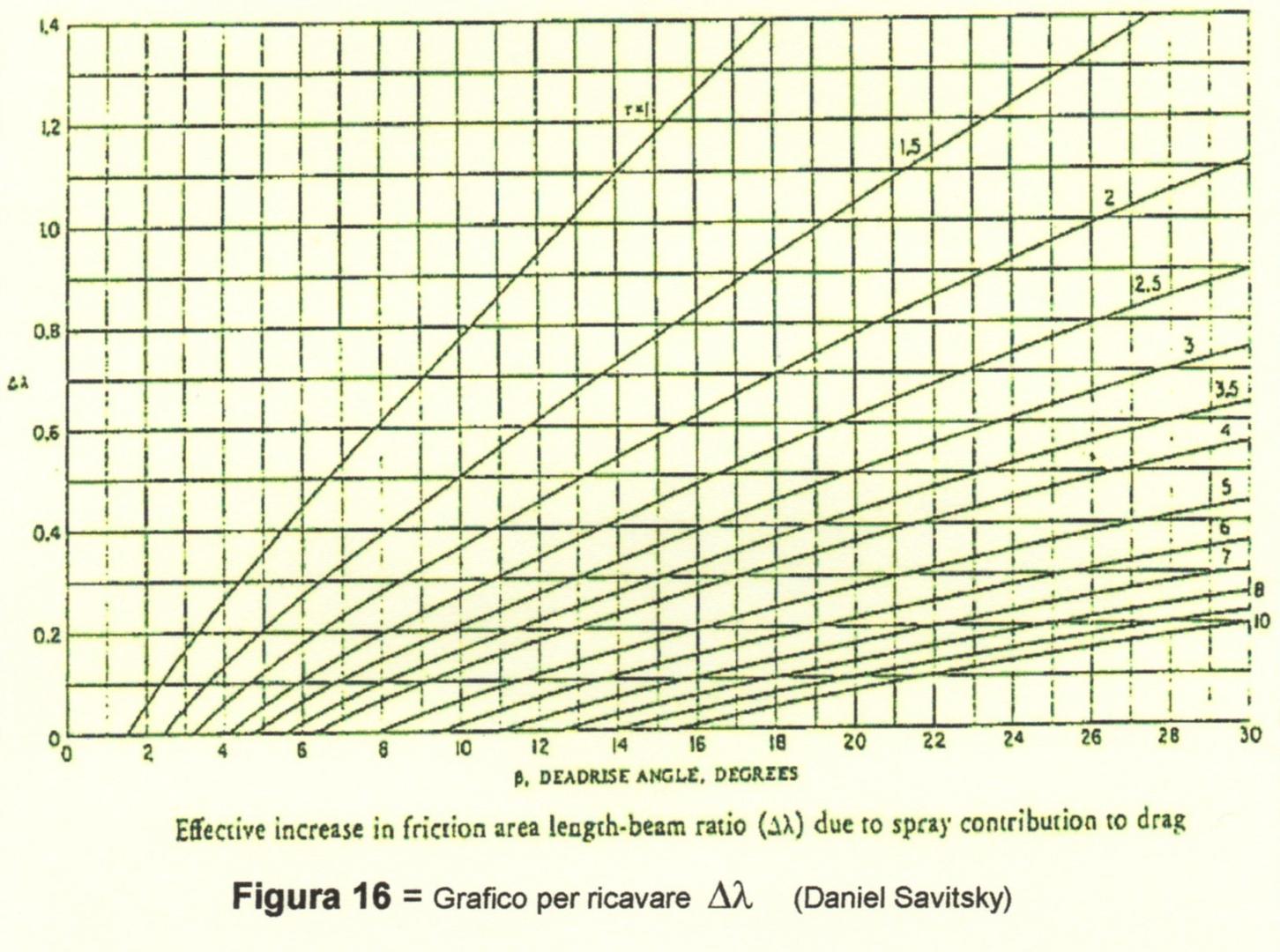
Il valore del rapporto di figura \(\Delta \lambda\) relativo alla superficie bagnata dagli spruzzi si può trovare sul grafico della Figura 16.
Per un valore dell’angolo di rialzo \(\beta=25°\) si può usare la seguente equazione
\(\Delta\lambda=2,1886 \cdot \theta^{-1,147}\)
Poiché la velocità dell’acqua sotto una carena in planata varia tra la chiglia e lo spigolo, dobbiamo necessariamente trovare la velocità media, che è data
\(V_m= V \cdot \sqrt{1- (C-0,0065 \cdot \beta \cdot C^{0,6}/( \lambda \cdot cos \theta ) }\) |
\(C= 0,012 \cdot \sqrt{\lambda} \cdot \theta^{0,1}\) | |||
dove |
\(V_m\) velocità media |
|||
|
|
\(V\) = velocità dello scafo |
|||
|
|
\(\beta\) = angolo di rialzo del fondo dello scafo |
|||
|
|
\(\theta\) = angolo di assetto in corsa |
|||
|
|
\(\lambda\) = rapporto di figura |
|||
Ci sono diversi metodi per calcolare il coefficiente di attrito \(C_F\), quello adoperato dalla I.T.T.C. 1957 è
Il numero di Reynolds è
\(R_n= (V_m \cdot L_m)7 v\) |
|||
dove |
\(V_m=\) velocità media |
||
|
|
\(L_m\) = lunghezza media della figura bagnata sotto carena |
||
|
|
\(v\) = coefficiente di viscosità cinematica |
||
Considerando un aumento di resistenza di attrito \(\Delta C_F= 0,0004\), dovuto alla non perfetta superficie levigata del fondo, si avrà
\(R_F= \frac{1}{2} \cdot \rho \cdot (V_m^2 \cdot A + V^2 \cdot A_S) \cdot (C_F +\Delta C_F)\)
Le appendici di carena sono costituite da: timone, assi porta elica, bracci porta elica, astucci, prese di acqua di mare e qualsiasi altra protuberanza che esca sotto il fondo della carena. La resistenza delle appendici di carena \(R_{APP}\), con l’aumentare della velocità diventa sempre più consistente, inoltre il braccio porta elica crea un disturbo sempre maggiore all’elica. Infatti superata la velocità di circa 40 nodi è necessario eliminare tutte le appendici ed usare come propulsore l’elica semisommersa o l’idrogetto. Il Lindsay Lord afferma che una buona previsione della resistenza delle appendici può essere eseguita in funzione dell’area proiettata trasversale delle appendici stesse e della pressione statica agente sul loro centro di figura.
Per cui
\(R_{APP}= p_s \cdot A_t \cdot V^{1,83} \cdot 0,001\) |
|||
dove |
\(p_s=\) \((34+ H) \cdot 0,4444\)libbre per pollice quadrato |
||
|
|
\(A_t\) = area trasversale delle appendici in pollici quadrato |
||
|
|
\(H\) = immersione del centro dell’area trasversale in piedi |
||
|
|
\(V\) = velocità dello scafo in nodi |
||
La resistenza dovuta all’aria e vento, sebbene non trascurabile, è contenuta entro valori non eccessivi fino a che la velocità non supera i 30÷40 nodi. Al di sopra di questa velocità la resistenza \(R_A\) comincia ad avere valori consistenti. Contrariamente a quanto si possa pensare, l’effetto del vento spirante nella direzione contraria al moto non è mai così nocivo come quello spirante in direzione laterale. In altre parole il profilo longitudinale dell’opera morta ha più influenza sulla resistenza e sul comportamento generale dell’imbarcazione che la meno estesa forma trasversale.
Il vento proveniente con un certo angolo rispetto alla direzione del moto non solo tende a portare la prora fuori rotta con conseguente aumento della resistenza al moto, dovuto alla necessaria azione del timone ma anche a provocare nell’imbarcazione nocivi angoli di sbandamento.
La resistenza dell’aria per una nave a dislocamento rappresenta una piccola parte della resistenza totale. Per uno scafo planante veloce, detta resistenza costituisce invece un fattore molto importante e talvolta è accompagnata da notevoli forze verticali. Bisogna tenere presente che con l’aumentare della velocità aumentano nello scafo planante le superfici esposte all’aria in conseguenza dell’innalzamento che subisce l’imbarcazione. Tutto questo accentua la necessità di mantenere una buona visibilità a prora, nonostante l’angolo di assetto assunto in corsa.
La resistenza al vento è data da
\(R_A= K \cdot A_p \cdot V_{RV}^2\) |
|||
dove |
\(R_A=\) resistenza dell’aria o del vento |
||
|
|
\(K\) = costante |
||
|
|
\(A_p\) = area proiettata del profilo dell’imbarcazione su un piano normale alla direzione del vento |
||
|
|
\(V_{RV}\) = velocità relativa del vento |
||
La resistenza totale è
\(R_T= R_R + R_F + R_{APP} + R_A\)
Nella sesta parte oltre al calcolo della potenza sarà esplicitato il calcolo delle accelerazioni.
©PressMare - riproduzione riservata





