Le forme della carena tonda - quarta parte

Come solitamente avviene nella progettazione, la ricerca di tutti i parametri geometrici definitivi, indispensabili al disegno del piano di costruzione, avviene in successive fasi di affinamento in relazione a tutte le esigenze specifiche del progetto.La parte riguardante la geometria della carena è intesa nell’ottica di un impiego iterativo, non solo in relazione a problemi di stabilità e di sistemazioni interne, ma soprattutto per la possibilità di affinare le grandezze geometriche che maggiormente influenzano la resistenza al moto.

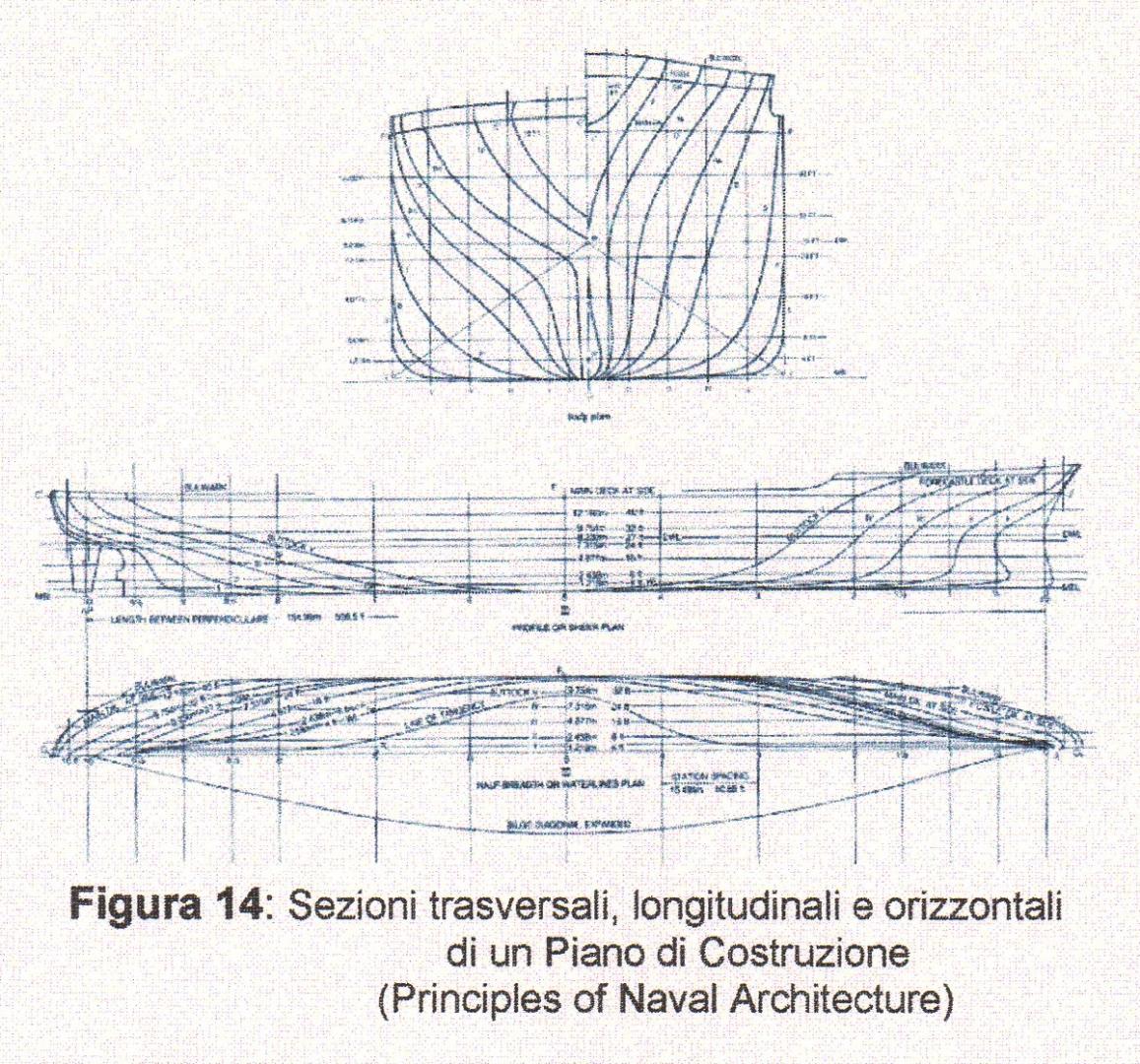
Nelle parti precedenti dell’articolo, già pubblicate, sono stati descritti il primo e il secondo metodo per la scelta della carena. In questa quarta parte dell’articolo sarà esplicitato il terzo metodo. Attualmente il sistema che dà risultati più attendibili per uno studio del comportamento della nave è l’uso dei modelli. Il modello di una nave si costruisce dopo aver realizzato il piano di costruzione della nave (Figura 14), che può essere definito dopo aver trovato le dimensioni principali e tutti i coefficienti idrodinamici della carena. Se la similitudine non è possibile, dobbiamo necessariamente realizzare un piano di costruzione della nave per verificare il volume necessario, richiesto dal progetto operativo, per trovare la resistenza totale a una velocità stabilita e conseguentemente la potenza necessaria.

Se ricaviamo la nuova carena da un’altra esistente, anche se quest’ultima è una carena valida alla sua velocità di progetto, non è assolutamente certo che la nuova carena sia valida a una velocità relativa diversa.

Quindi per trovare questa nuova forma di scafo dobbiamo fare una ricerca di carena adoperando una serie sistematica. In questo modo possiamo dire che lo studio della nuova carena sarà il miglior compromesso possibile, poiché il confronto sarà fatto con una carena provata in vasca, che deriva da una famiglia di carene. 

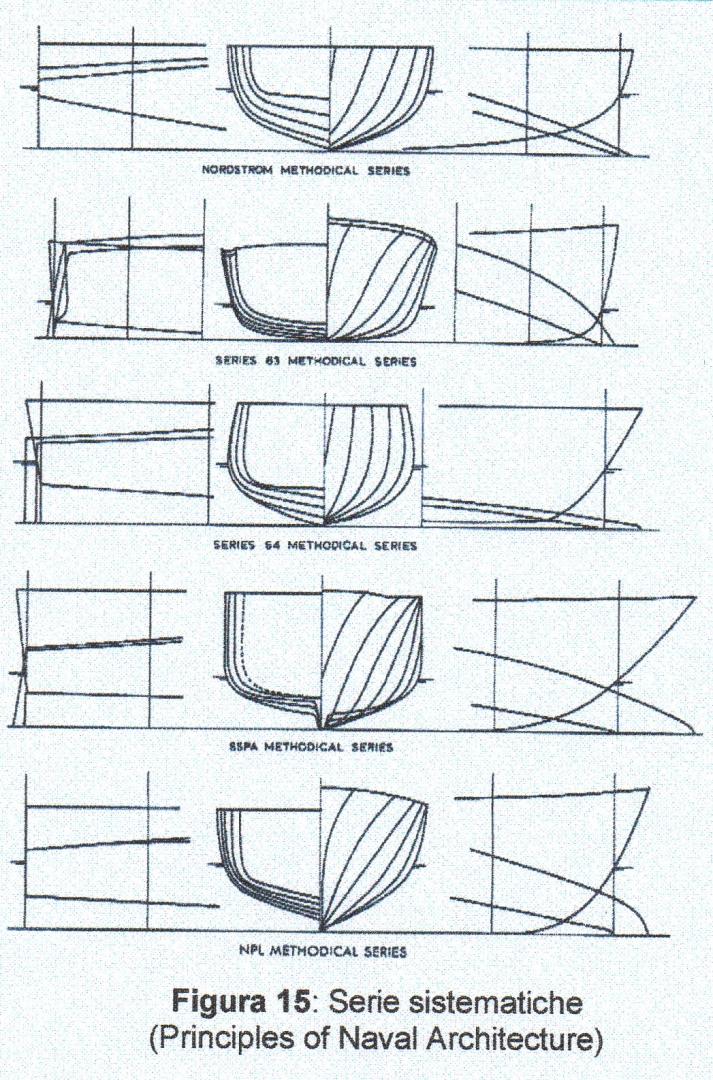
Facendo ricorso a carene delle Serie Sistematiche (Figura 15) sperimentate da alcune Vasche Navali come:

- Serie sistematiche di Taylor, eseguita dall’ammiraglio Taylor all’Experimental  Model Basin di Ashington, valide fino a velocità relative \(T_q=(V/\sqrt{L_{WL}})=2;\)

- Serie  60 di  F. N. Todd adatta per navi mercantili monoelica \((C_B=0,6\div0,8);\)

- Serie 64, con la richiesta di maggiore velocità. Nel 1959 il David Taylor Model Basin realizzò un’estensione della serie di Taylor per valori più alti di \(T_q\), fino a raggiungere il valore di 5, con la scelta di tre parametri fondamentali \(C_B, \Delta/(0,01 \cdot L_{WL})^3, B_{WL}/H\) e il coefficiente prismatico costante \(C_p= 0,63;\)

- Serie NPL;

- Serie Nordstrom;

- Serie 63;

- Serie SSPA.

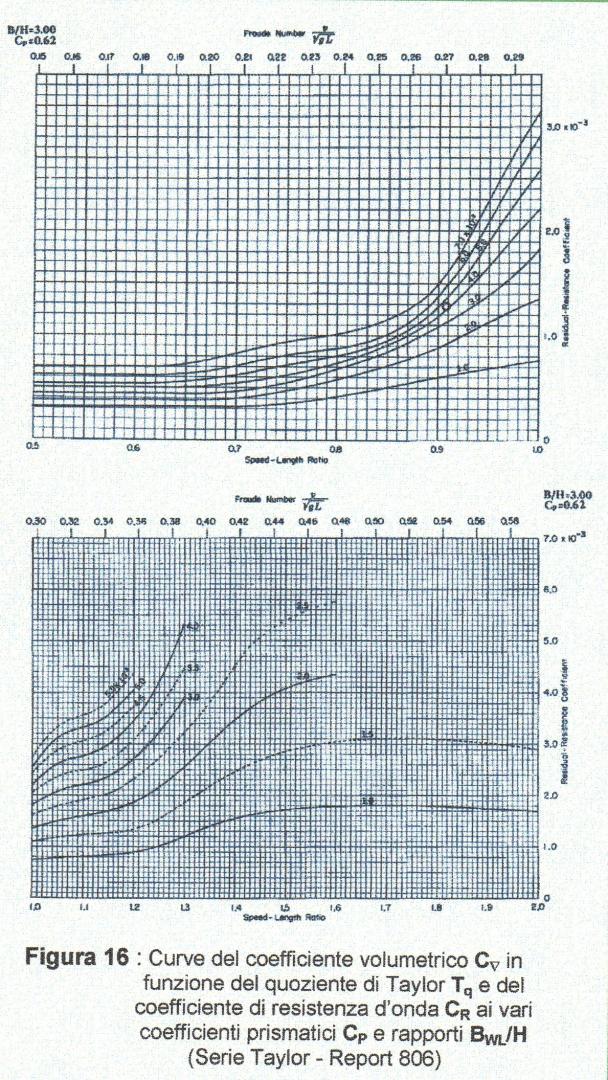
La serie di Taylor, ancora oggi, è ritenuta la più completa ricerca degli effetti sulla \(P_E\) (potenza effettiva) al variare di alcuni coefficienti e di rapporti significativi di una carena madre. I dati furono presentati come curve di resistenza residua (Figura 16). Essa fu misurata in libbre per tonnellate di dislocamento in funzione del coefficiente prismatico \(C_P\) e del rapporto di dislocamento/lunghezza \(\Delta/(0,01\cdot L_{WL})^3;\) ciascun diagramma è valido per rapporti di larghezza/immersione \((B_{WL}/H)\) e velocità/lunghezza \((T_q).\) Taylor esaminò ottanta modelli e dai valori di resistenza totale, ottenuti dalle prove di questi modelli, sottrasse la resistenza di attrito calcolata secondo la formula di Tideman.

Per avere un’idea della ricerca di carena, utilizzando la serie sistematica di Taylor, fissato un dislocamento a pieno carico, come se l’esponente di carico fosse stato già fatto, una lunghezza tra le perpendicolari uguale a quella al galleggiamento ed una velocità operativa, avremo per esempio

Con il quoziente di Taylor utilizzando la Figura 7 possiamo ricavare un valore approssimativo del coefficiente prismatico longitudinale \(C_P\), in funzione del quoziente di Taylor \(T_q=(V/\sqrt{L_{WL}})\)

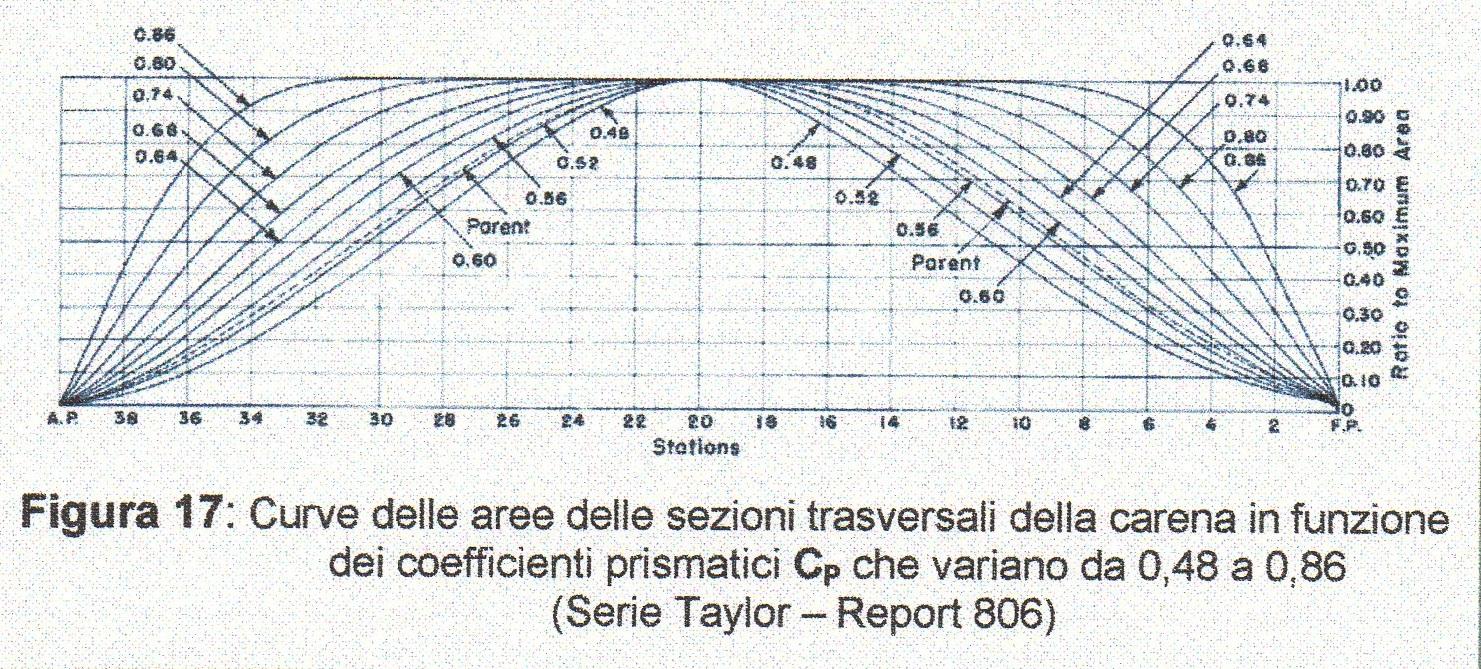
Questo coefficiente è molto importante perché determina la distribuzione delle aree delle sezioni trasversali della carena (Figura 17). Quindi è molto utile ottimizzarne il valore in funzione della velocità e della lunghezza. Il parametro \(T_q\) è chiamato anche “velocità relativa alla lunghezza della nave”.

Utilizzando il grafico della Figura 7, in funzione del rapporto \(T_q\), otteniamo che il coefficiente \(C_p\) può variare tra 0,6 e 0,63 e che, in funzione del coefficiente di snellezza

\(\frac{\Delta}{(0,1\cdot L_{WL})^3}=\frac{1650}{(0,1\cdot 92)^3}=2,1\)

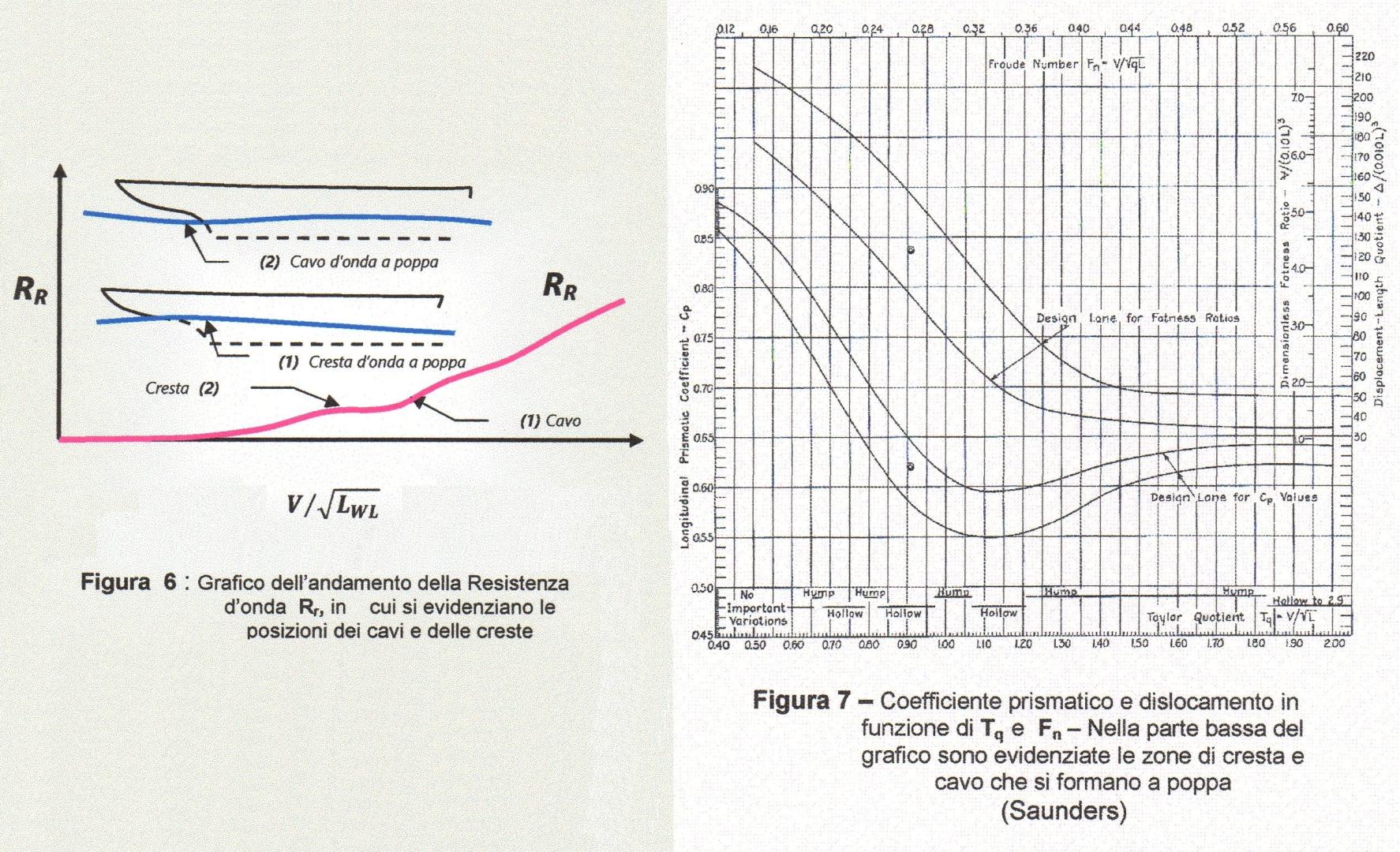
possiamo verificare che il dislocamento è un buon compromesso relativamente alla velocità e alla lunghezza della nave, poiché siamo vicini al valore massimo della zona ottimale. Inoltre siamo in una zona di cresta, cioè a poppa abbiamo una formazione ondosa favorevole alla resistenza della nave (Figura 6).

Nella prossima parte dell’articolo si proseguirà con la ricerca di carena.

Angelo Sinisi