Le forme della carena tonda - prima parte

Nell’articolo precedente “La ricerca e lo sviluppo delle forme della carena” sono state evidenziate le differenze tra una carena dislocante ed una planante e le condizioni idrodinamiche, stabilite dal progetto operativo, che determinano la scelta dell’una o dell’altra carena.

Il progetto di una nave è il risultato di un lungo processo iterativo in cui concorrono le esigenze specifiche della costruzione in esame e le esperienze precedentemente acquisite. Il progettista si deve basare principalmente sulla scelta più idonea delle dimensioni e della forma della carena allo scopo di raggiungere sia il rendimento propulsivo ottimale, a vantaggio del risparmio di combustibile o della velocità, sia il miglior compromesso tra i requisiti di servizio e il peso minimo a nave scarica ed asciutta.

Il compito fondamentale del progettista della carena è quello di adottare dimensioni e coefficienti idrodinamici che rendano minima  o comunque limitino la resistenza di attrito e la resistenza d’onda, che sono le due principali forze che costituiscono la resistenza totale della carena. Per quanto riguarda la resistenza d’attrito il discorso è relativamente semplice, poiché essa dipende soprattutto dalla superficie di carena, dalla sua rugosità e dal suo stato di pulizia e potrà essere facilmente controllata operando su tali parametri.

Al fine di prevenire la formazione di sporcizia, dovuta a vegetazione marina e a micro organismi che si formano dopo lunghi periodi di permanenza in mare, soprattutto in acque calde, la superficie dell’opera viva è trattata con pitture antivegetative speciali. La quantità di sporcizia può portare ad aumenti sensibili di resistenza. Periodicamente queste pitture devono essere rinnovate, da cui la necessità di periodiche permanenze in bacino di carenaggio.

Più complicato è invece il discorso sulla resistenza d’onda, perché su di essa ha notevole influenza la forma della carena, cioè, i vari coefficienti idrodinamici e soprattutto la lunghezza relativa alla velocità. A questo proposito è utile un richiamo alla formazione ondosa e in particolare al tipo più comune di configurazione di onda creata dal moto della nave.

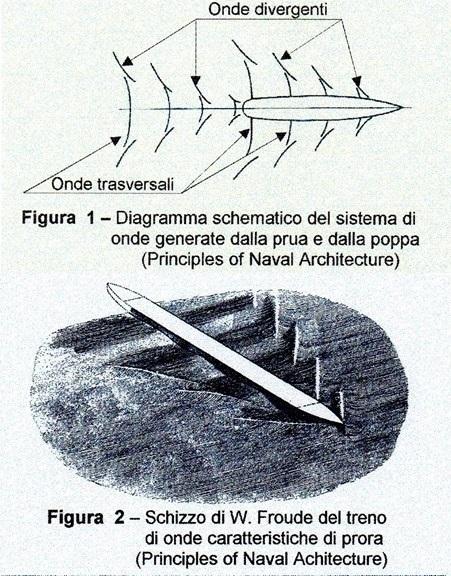
Un corpo che si muove sulla superficie indisturbata dell’acqua produce un sistema d’onde. Questo sistema è generato dal campo di pressioni intorno al corpo e l’energia posseduta dalle onde è ceduta dal corpo stesso. Questo trasferimento di energia, dal corpo al sistema circostante, genera una forza di direzione opposta a quella del moto, che è appunto la resistenza d’onda.

Le onde generate dalle navi sono di due tipi, quelle divergenti, che si formano lateralmente alla nave e che hanno creste inclinate rispetto al piano di simmetria nave, e quelle trasversali che si formano sulla murata della nave e che hanno le creste perpendicolari alla mezzeria (Figura 1 e Figura 2). Tale sistema di onde, divergenti e trasversali, è generato sia dalla poppa sia dalla prora. La Figura 3 è una bella e caratteristica foto che mostra questo sistema di onde. L’interferenza tra questi sistemi d’onda crea la formazione ondosa con le caratteristiche gobbe e cavi in funzione del rapporto velocità/lunghezza \((V/L_{WL})\) (Figura 4).

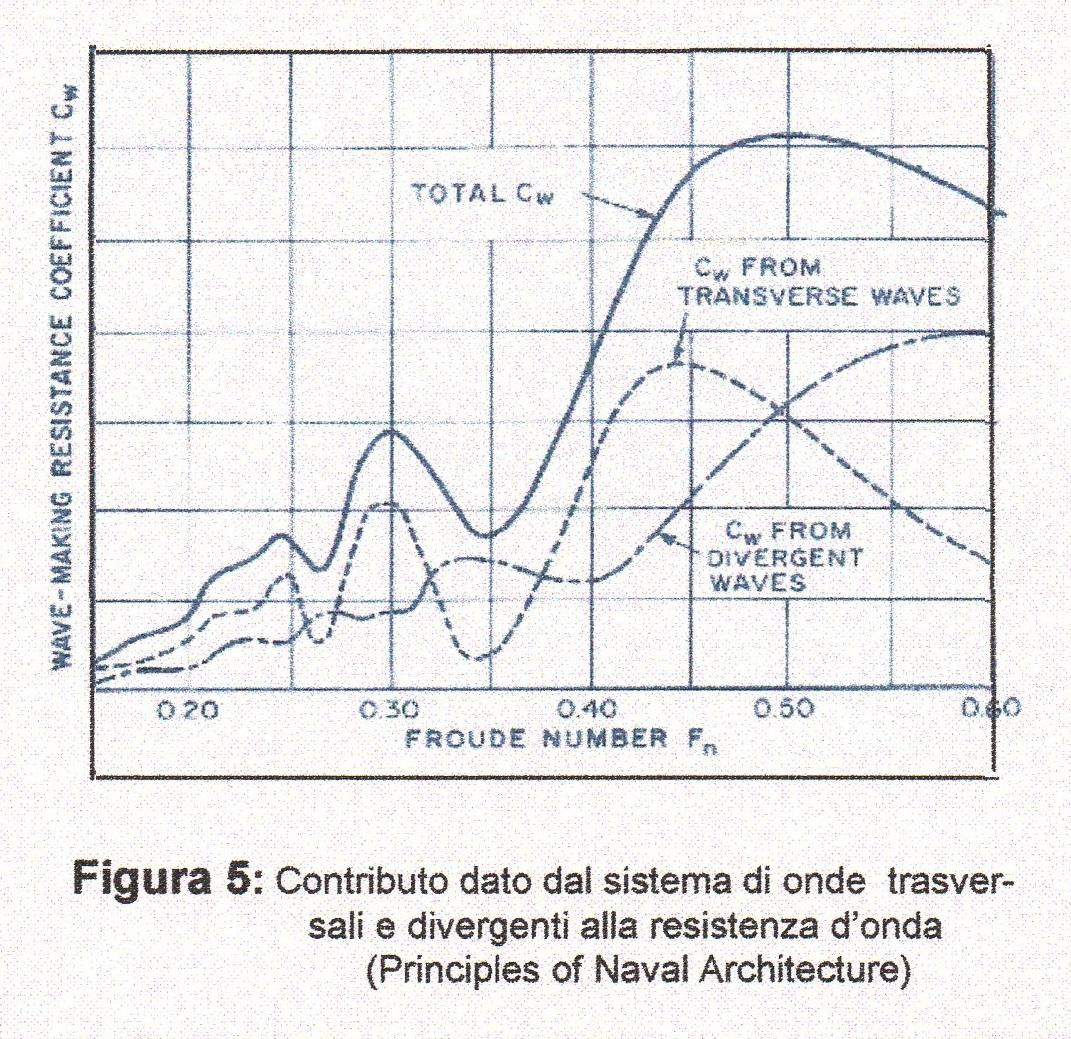
Il ricercatore inglese WIGLEY fece uno studio per dimostrare il contributo dato dalla formazione ondosa sia dal sistema di onde trasversali che da quello di onde divergenti. Dimostrò che, fino a valori del numero di Froude Fn=0,45 , il maggiore contributo alla formazione ondosa è dato dal sistema di onde trasversali, causa dei cavi e delle gobbe della resistenza nella curva della resistenza d’onda. Sopra questo valore del numero di Froude, il contributo delle onde divergenti diventa sempre più grande,  come si nota nella Figura 5. 

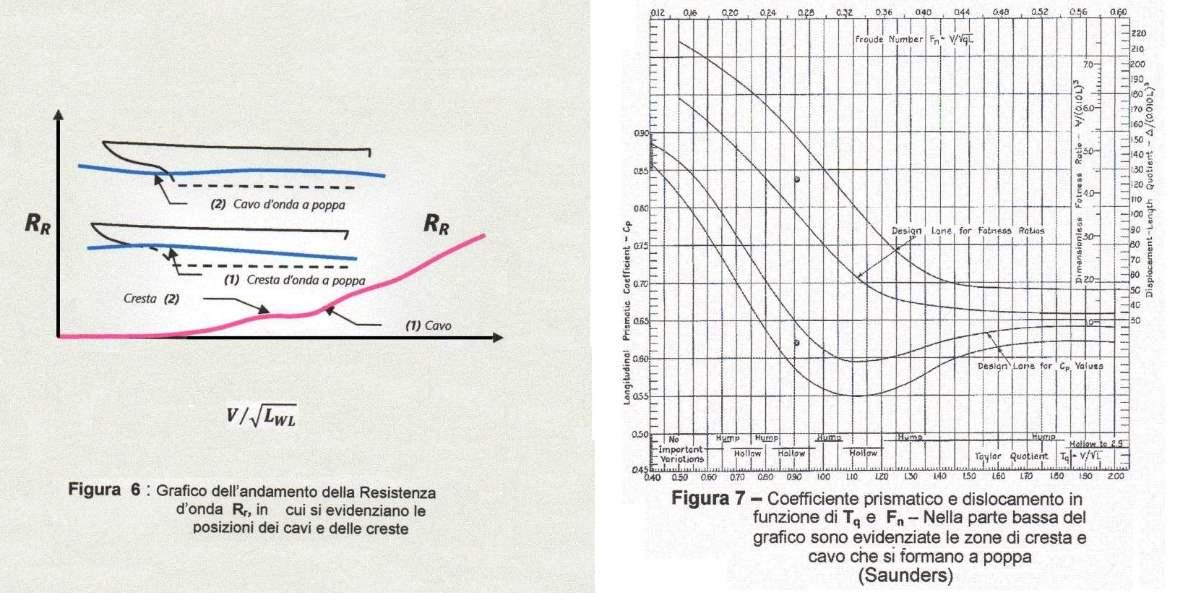
Considerando solamente le onde trasversali, in modo semplicistico ma indicativo, si può dire che la resistenza d’onda è data dalla differenza fra le pressioni che si hanno nella zona prodiera, dirette nel senso prora→poppa, e le pressioni che si hanno nella zona poppiera, che hanno risultante opposta nel senso poppa→prora. Mentre il sistema di pressioni prora→poppa cresce costantemente al crescere di \(V/L_{WL}\), il sistema di pressioni poppa→prora è oscillante (cioè può essere positivo o negativo) a seconda dell’interferenza fra i sistemi d’onda di prora e di poppa. Si avrà, quindi, una gobba della resistenza d’onda quando a poppa vi è un cavo (d’onda), e, viceversa, un cavo quando a poppa vi è una cresta (d’onda) (Figura 6). Inoltre nella Figura 7, nella parte bassa del grafico, sono ben evidenti le zone di cavo e di cresta, in funzione \(V/ \sqrt{L_{WL}}\) che si formano a poppa. Pertanto il fattore più importante per la resistenza d’onda è il rapporto \(V/ \sqrt{L_{WL}}\) conosciuto col nome di quoziente di Taylor oppure \(V/ \sqrt{g\cdot L_{WL}}\) noto come numero adimensionale di Froude. Vediamo come nasce questa dipendenza della formazione ondosa dal suddetto quoziente di Taylor.

La formazione ondosa, creata dal moto della nave, si muove alla velocità della nave, anche se nel suo insieme non si muove. Si ritiene inoltre che la velocità della nave e della formazione ondosa siano uguali a quella definita dalla teoria trocoidale per la velocità dell’onda e cioè

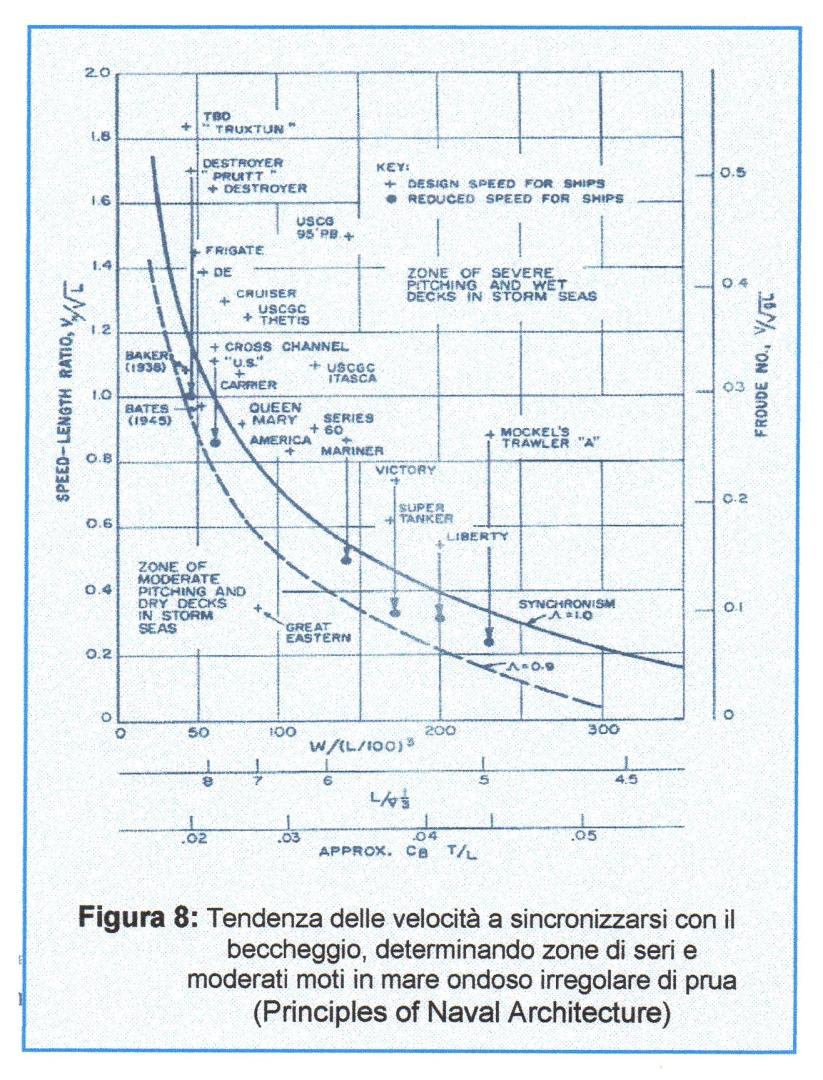
cioè se è costante il quoziente di Taylor è anche costante il rapporto di lunghezza d’onda e di lunghezza di carena. Da questa relazione discende una considerazione fondamentale da tenere presente nella progettazione delle navi a dislocamento: una nave, se deve essere veloce, dovrà essere la più lunga possibile, in quanto essa non solo incontrerà una minore resistenza d’onda, ma avrà anche maggiori prestazioni di tenuta al mare, come si può notare dalla Figura 8.

Quali sono le voci di un esponente di carico? Quali sono i metodi usati per la scelta della carena? La prossima parte di questo articolo cercherà di rispondere a queste domande.

 Angelo Sinisi