
La Nave scuola Amerigo Vespucci (© Marina Militare)
Le condizioni evolutive delle navi: la terza fase della manovra di evoluzione
Dopo aver parlato della prima e seconda fase della manovra di evoluzione ora tratterò la terza fase della manovra di evoluzione e gli effetti negativi del timone.
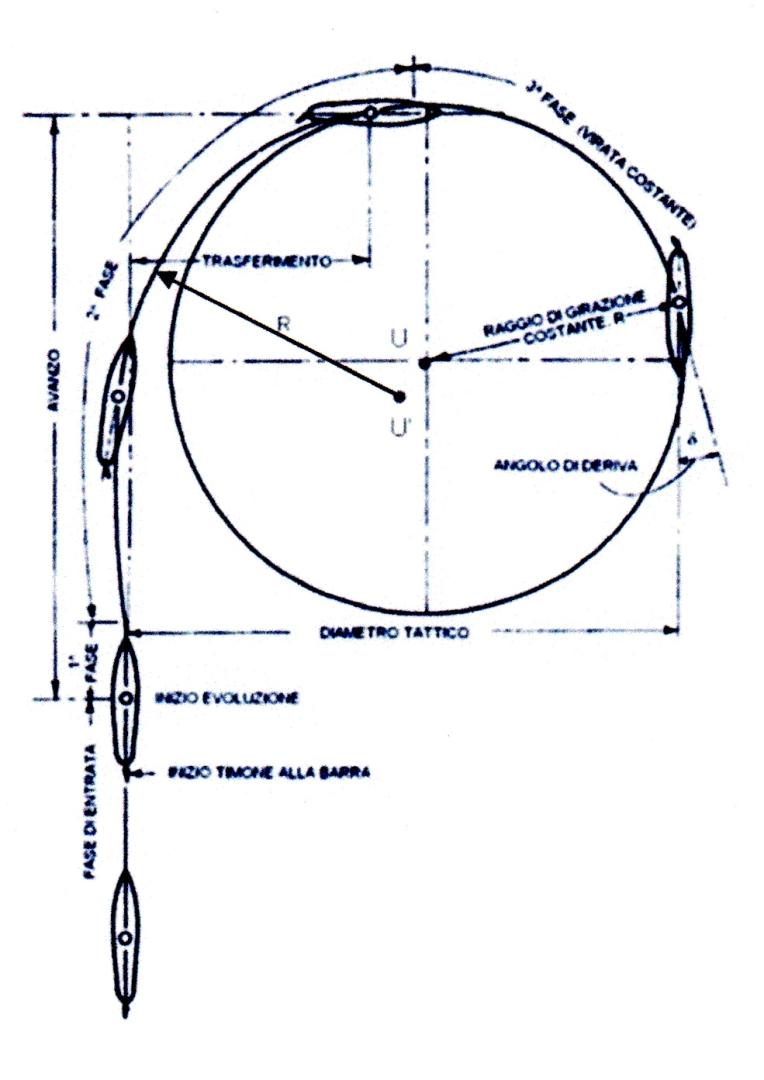
3a fase della manovra di evoluzione (Figura 3)
Le accelerazioni angolari positive e negative in direzione opposta a quella della velocità tangenziale \(V_t\) (Figura 5) cessano entrambe, mentre la forza centrifuga è bilanciata dalle forze idrodinamiche che nascono nel moto. Il raggio di curvatura \(R\) diventa costante ed il centro di gravità della nave traccerà un cerchio di evoluzione. La velocità della nave, diminuita durante le due prime fasi, a causa dell’aumentata resistenza idrodinamica e della forza generata dal timone, rimane costante. La terza fase si raggiunge generalmente dopo una variazione di rotta di circa 100°÷120° gradi dalla rotta originaria.
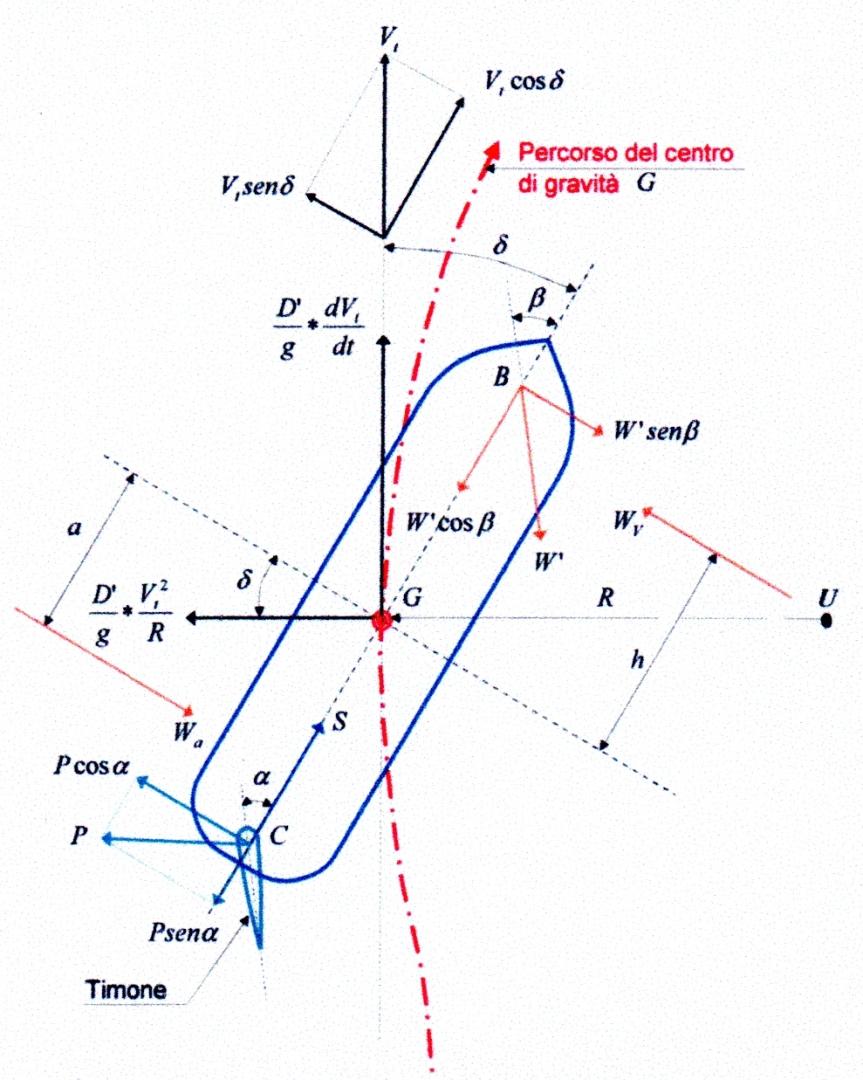
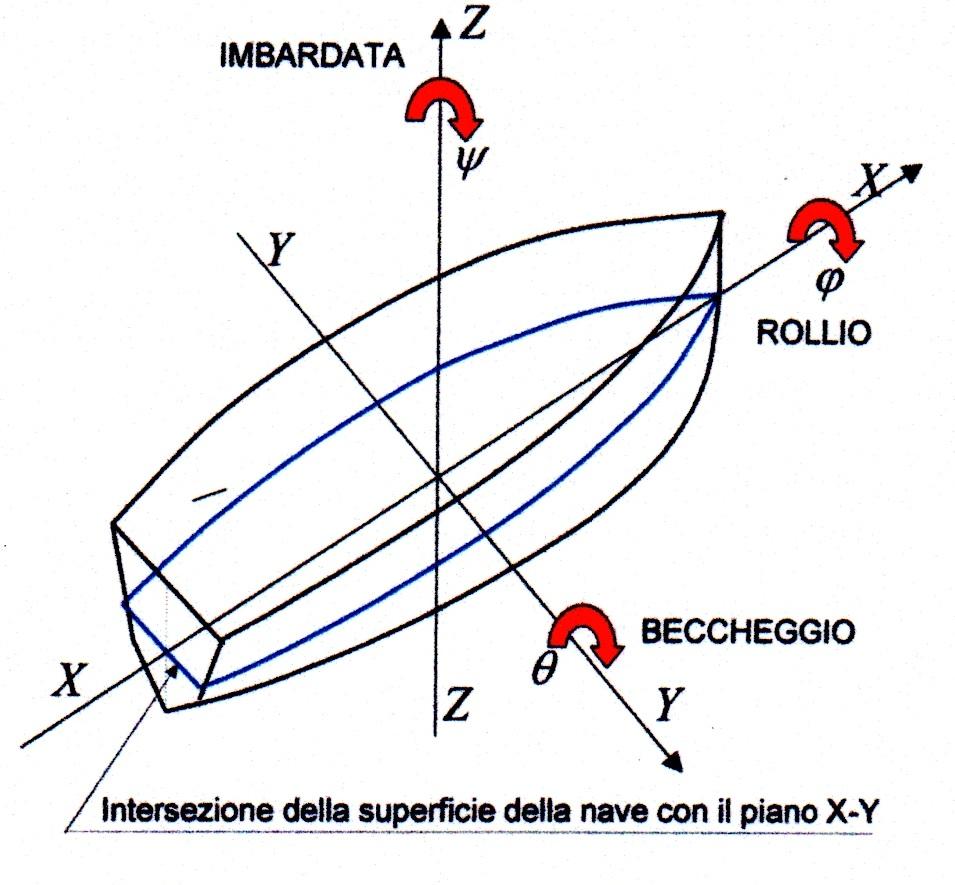
Uno dei risultati secondari indesiderabili dell’uso del timone è lo sbandamento della nave intorno ad un asse longitudinale \(X\) (Figura 1). Ciò è dovuto al fatto che le forze trasversali agiscono su posizioni verticali diverse. Inoltre queste forze variano col passare della nave attraverso la prima e la seconda fase, cosicché lo sbandamento dipende, in ciascun istante, dalla fase nella quale si trova la nave in quello stesso istante (Figura 4).
Nella prima fase le forze trasversali agenti (Figura 4) sono la componente della forza generata dal timone \(P \cdot cos \alpha\) e poi la componente della resistenza \(W' \cdot sin \beta\) . Poiché la resistenza \(W' \cdot sin \beta\) è piccola all’inizio dell’evoluzione, e quindi di lieve importanza, \(P \cdot cos \alpha\) causa uno sbandamento, formando l’angolo \(\varphi_1\) (Figura 4), verso dritta quando si mette la barra a dritta e viceversa. La forza \(W' \cdot sin \beta\) aumenta allora gradatamente e lo sbandamento diminuisce lentamente.
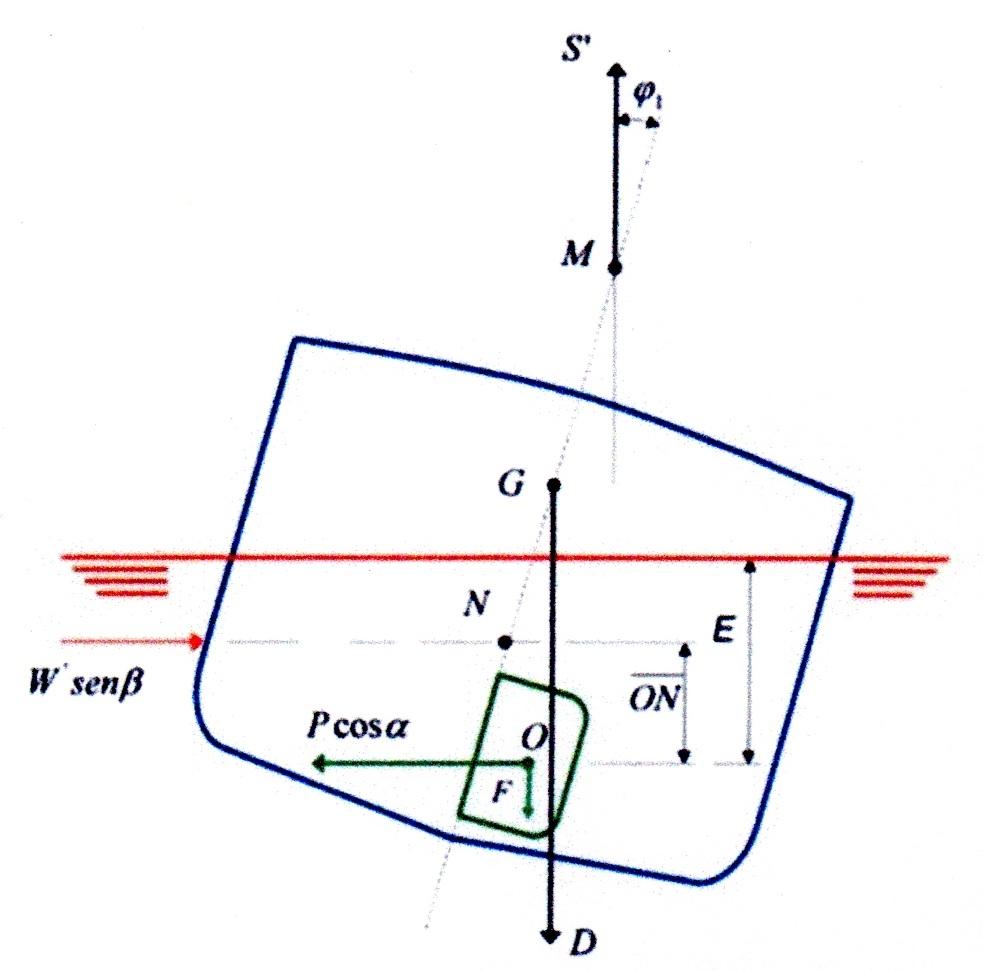
Come si vede dalla Figura 4, il punto di applicazione della forza \(P \cdot cos \alpha\) si trova sotto quello di \(W' \cdot sin \beta\) in quanto quest’ultima forza agisce in corrispondenza o leggermente sopra il baricentro del piano di deriva (che è la proiezione longitudinale della carena immersa). Per piccoli angoli di sbandamento si può supporre che l’asse attorno al quale la nave ruota giaccia nell’intersezione del piano di galleggiamento con il piano longitudinale di simmetria (Figura 1).
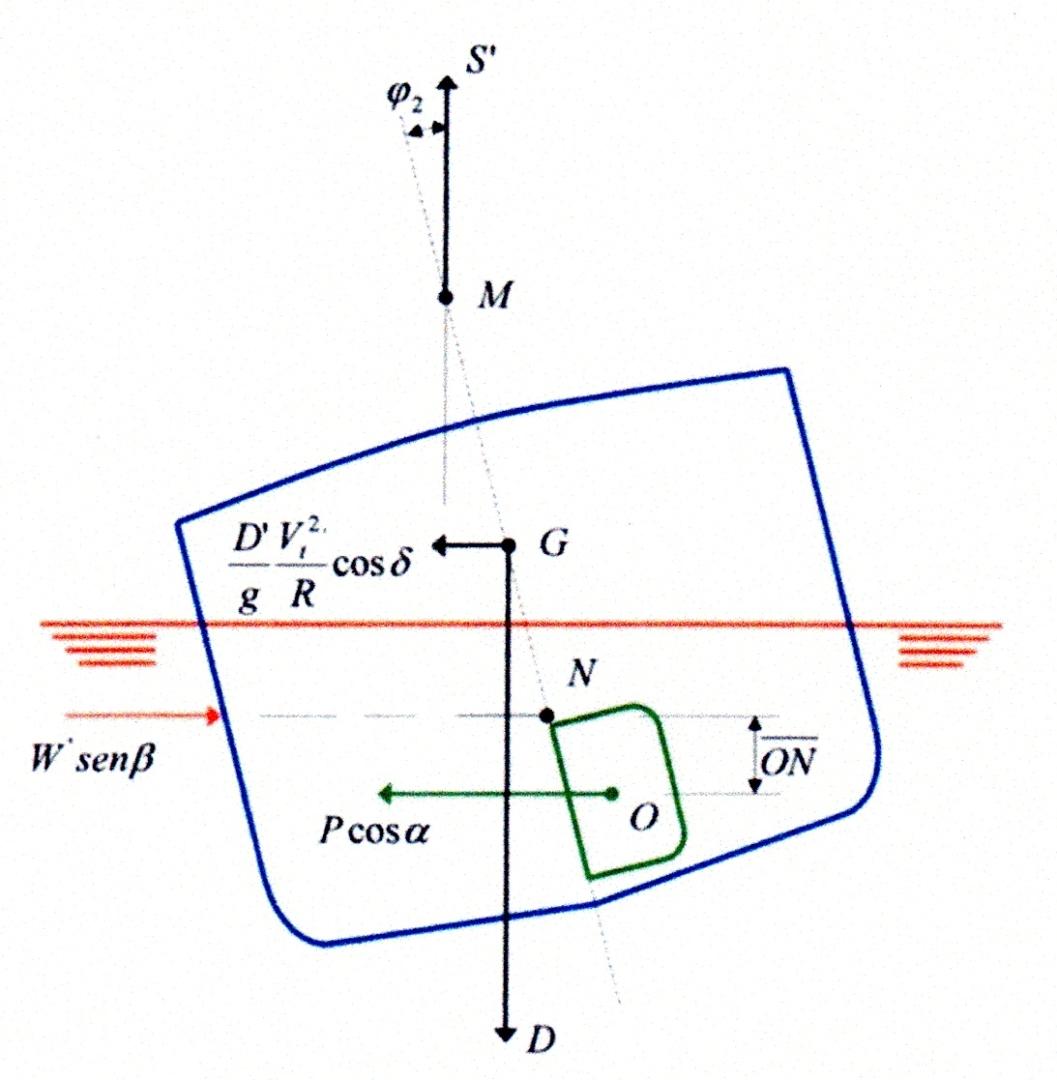
Non appena la nave inizia a girare nella seconda fase intorno al centro istantaneo \(U'\) , entra in gioco la componente trasversale \({D ' \over g} \cdot { V_t^2 \over R} \cdot cos \delta\) ( \(\delta\) = angolo di deriva Figura 5) della forza centrifuga (Figura 7). Per cui la nave tenderà a sbandare sulla sinistra se nella prima fase è stata messa la barra a dritta e viceversa.
L’angolo di sbandamento \(\varphi_2\) (Figura 7) maggiore si raggiunge immediatamente dopo il cambiamento di sbandamento da dritta a sinistra, poiché, a causa della sua inerzia di massa, la nave sbanda al di là della sua posizione di equilibrio statico.
Angelo Sinisi








