Il progetto idrodinamico del timone: il rapporto di figura e i vari coefficienti

Uno dei dati caratteristici del timone è il rapporto di figura \(a\), che è definito come il rapporto tra l’altezza \(b\) del timone e la sua corda media \(c_m\) (Figura 12).

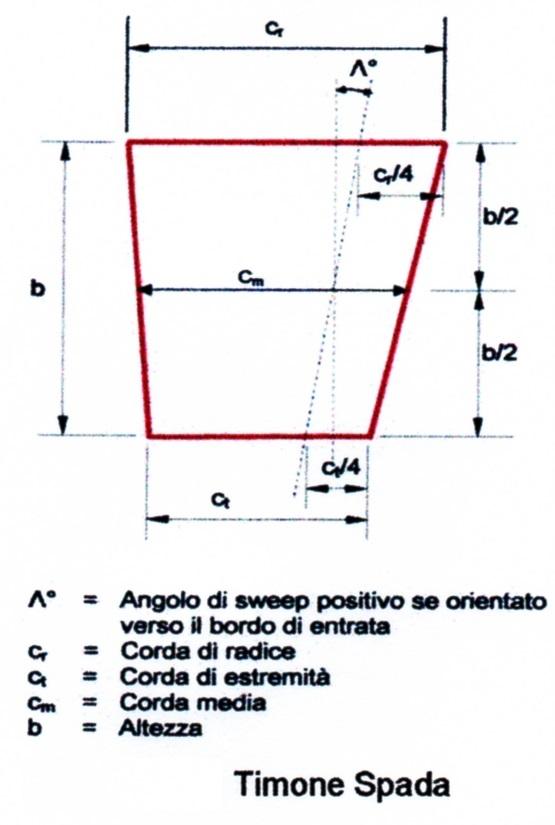
Il rapporto di figura geometrico o allungamento geometrico del timone è dato da

\(a_g = {b \over c_m} = {b^2 \over b \cdot c_m} = {b^2 \over A_R}\)

dove

\(b\) = Altezza del timone

\(c_m\) = Larghezza media del timone

\(A_R\) = Area del timone proiettata = \(b \cdot C_m\)

Il rapporto di figura influisce notevolmente sul coefficiente di portanza totale perché da esso dipende la maggiore o minore influenza del cosiddetto effetto di estremità. Per questo motivo nel caso in cui il timone sia con la sua estremità superiore a stretto contatto con una lastra piana, si usa considerare il rapporto di figura effettivo che vale il doppio di quello geometrico, cioè:

\(a_e = {(2 \cdot b^2) \over A_R}\)

ma per vari motivi e specialmente di carattere costruttivo si ha sempre uno spazio, tra la carena ed il timone, superiore \(a \)  \((b/15)\), per cui è nullo l’effetto della presenza della carena.

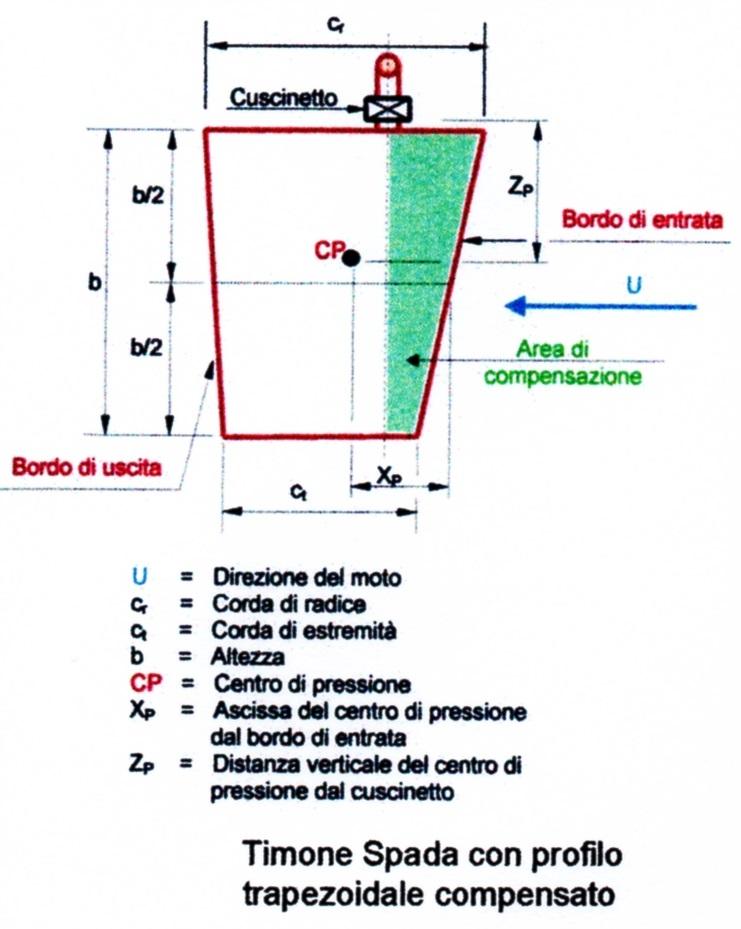
In fase di progettazione, quindi, è prudente assumere come allungamento effettivo l’allungamento geometrico. Inoltre se non vi è dello spazio tra la parte superiore del timone e la carena, in modo particolare alle alte velocità e in virata, si possono sviluppare delle forze verticali sotto la carena, tali da creare dei momenti sbandanti.

Il rapporto della corda di estremità \(c_t\) con la corda \(c_r\) alla radice del timone è comunemente detto rapporto di rastremazione (tape ratio) (Figura 11 e 12). Nella Figura 7 sono rappresentate le forze in gioco che devono essere prese in esame per studiare un timone. Tra i vari profili conosciuti, quelli più idonei a essere impiegati per la costruzione di un timone sono i così detti profili biconvessi simmetrici con linea d’asse rettilinea e coincidente con l’asse di simmetria. Un profilo di tal genere, immerso in una corrente fluida con velocità \(U\) e angolo di attacco \(δ_R\) come nella Figura 7, crea una dissimmetria nel campo delle velocità, per cui si ha un aumento di velocità sul lato sinistro (faccia passiva) ed una diminuzione sul lato dritto (faccia attiva) del timone.

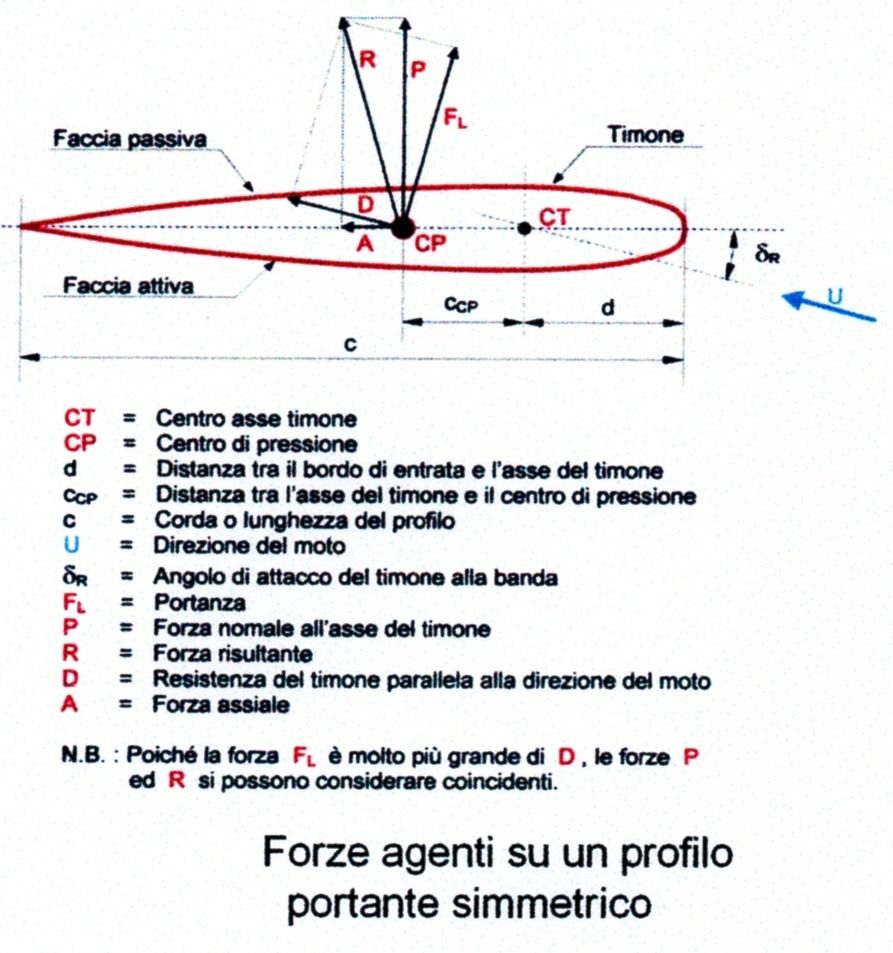
Secondo la legge di Bernoulli ciò dà luogo a una diminuzione di pressione sul lato sinistro e a un aumento di pressione sul lato dritto. La differenza di pressione produce una portanza \(F_L\) normale al vettore \(U\) , una resistenza \(D\) in direzione opposta al moto e la forza idrodinamica totale R (Figura 7), risultante delle due, o, in termini adimensionali, per profili simmetrici di allungamento finito si ha

un coefficiente di portanza \(C_L = F_L / ({1 \over 2} \cdot \rho \cdot A_R \cdot U^2)\)

un coefficiente di resistenza \(C_D = D / ({1 \over 2} \cdot \rho \cdot A_R \cdot U^2)\)

ed un coefficiente di forza idrodinamica totale \(C_W = R / ({1 \over 2} \cdot \rho \cdot A_R \cdot U^2)\)

dove

\(F_L\) = Portanza

\(D\) = Resistenza del timone parallela alla direzione del moto

\(R\) = Forza risultante

\(\rho\) = Densità del fluido

\(A_R\) = Area del timone proiettata

\(U\) = Velocità del fluido

In pratica per profili limitati, lavoranti in fluido reale come i timoni, si può scrivere:

\(C_L = (0,1 \cdot a \cdot \delta_R)/(a + 2,2 )\) e \(C_D = 0,011 + {\{[0,011 \cdot a \cdot {\delta_R}^2]/[\pi \cdot {(a + 2,2)}^2 ]\}}\)

dove

\(a\) = Rapporto di figura tra l’altezza del timone e la corda media (b/cm)

 \(\delta_R\) = Angolo di attacco della pala del timone in gradi

Nella quarta parte parlerò dell’areazione, della cavitazione e dell’angolo di stallo.

Angelo Sinisi