L’albero portaelica: il calcolo della sollecitazione statica

In questa seconda parte dell’articolo si parlerà del calcolo della sollecitazione statica che si verifica sull’albero portaelica. Da quanto detto nella prima parte si deduce che il calcolo di robustezza dell’asse portaelica per il momento torcente e flettente non sia sufficiente perché si deve verificare che i giri massimi dall’asse siano lontani dai giri critici.

La parte più importante di una linea d’asse (Figura 1) è l’albero portaelica, perché è soggetto a importanti sollecitazioni statiche e dinamiche. Conoscere il valore delle velocità critiche flessionali e la corretta sistemazione degli elementi indispensabili (posizione del braccio portaelica, dell’astuccio e dei cuscinetti (Figure 1 e 6) a una linea d’assi per una corretta trasmissione della potenza è molto importante per l’assenza di vibrazioni e di pericolose sollecitazioni anomale. Quindi il calcolo strutturale di un albero portaelica richiede un esame approfondito di tutte le cause che lo sollecitano contemporaneamente.

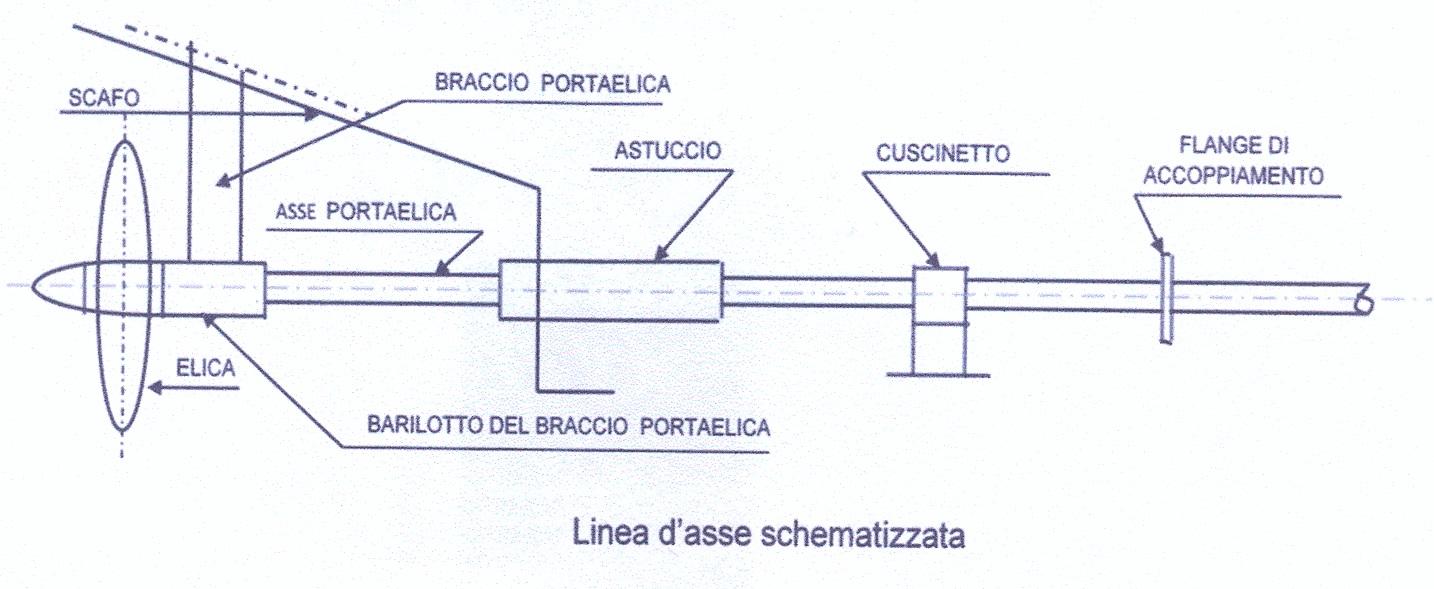
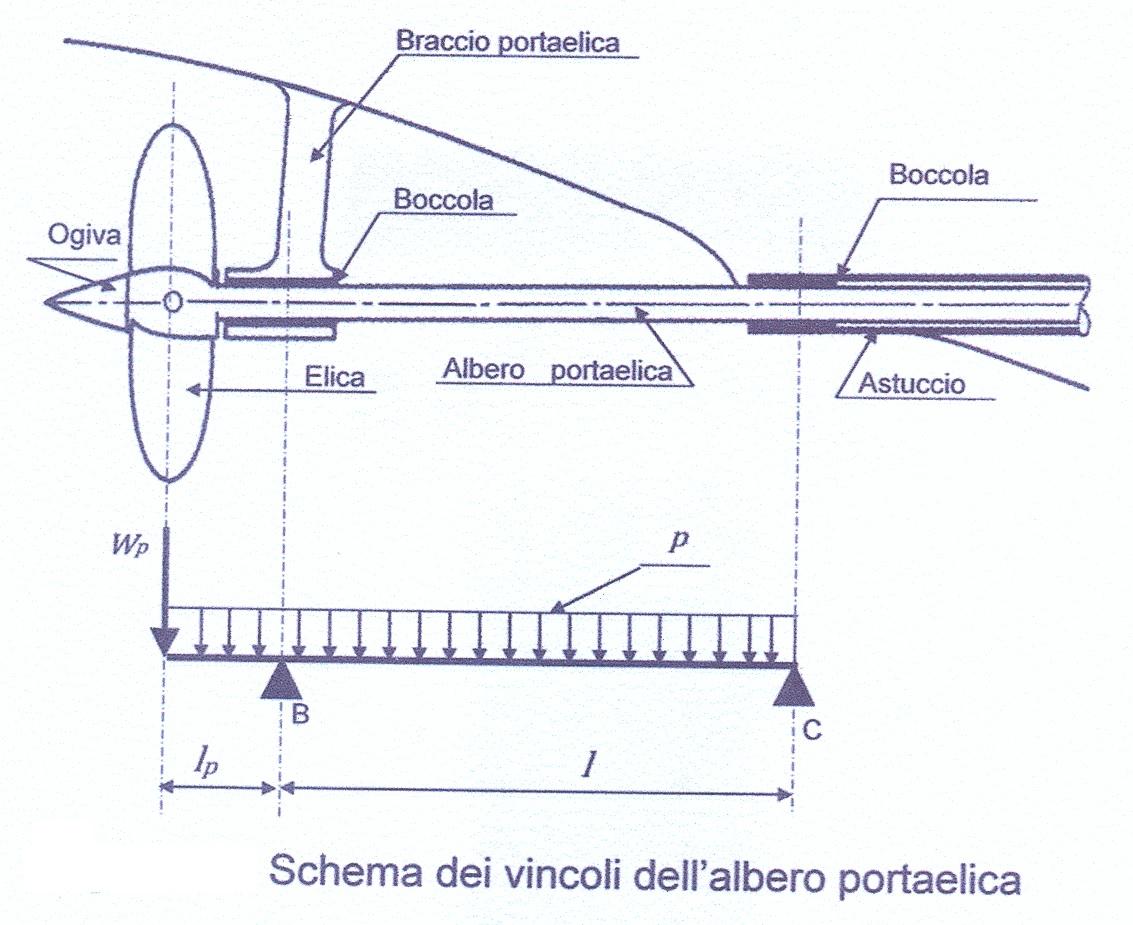
Il calcolo di robustezza dell’albero portaelica presuppone che la posizione degli appoggi (cuscinetti del braccio portaelica e dell’astuccio) sia definita (Figura 5). L’albero portaelica deve essere proporzionato per la massima potenza del motore considerando, però, un aumento del momento torcente di circa il 20%, che si può verificare quando nelle accostate i giri del motore diminuiscono.

Il momento torcente \(M_t\) ed il momento flettente \(M_f\), dovuto al peso dell’elica a sbalzo e alla spinta dell’elica, che data la sua sistemazione, non ha una spinta posizionata al centro, producono sollecitazioni alternate. Gli alberi che hanno un diametro inferiore a 150 mm sono a sezione piena, mentre quelli di diametro superiore hanno sezione forata.

Per semplificare il calcolo dei giri critici si può limitare lo studio a due campate, poiché non comporta variazioni apprezzabili dei risultati. Inoltre, aver considerato appoggi puntiformi (B e C Figura 5) invece che incastri imperfetti ed estesi per un certo tratto (lunghezza delle boccole Figura 5), è condizione più gravosa dei veri valori delle sollecitazioni.

Per il calcolo delle sollecitazioni statiche bisogna trovare:

 - il momento torcente, aumentato del 20%, in \(kg \cdot m\) da calcolare è

\(M_t = 716,2 \cdot {P_A \over N} \cdot 1,2\)

dove

\(P_A\) = potenza massima del motore in CV

\(N\) = numero di giri dell’asse al minuto primo

 - la sollecitazione tangenziale massima, se l’albero è cavo, è in \(kg / cm^2\)

\(\tau = {{M_t \cdot D \cdot 16 } \over {\pi \cdot (D^4 - d^4)}}\)

dove

\(D\) = diametro esterno dell’albero

\(d\) = diametro interno dell’albero

\(\pi\) = 3,1415927

se l’albero è pieno la sollecitazione massima tangenziale è

\(\tau = {{M_t \cdot 16 } \over {\pi \cdot D^3}}\)

La spinta dell’elica è data da

\(S = 145,7 \cdot \eta_e \cdot \eta_s \cdot {{P_D} \over V}\)

dove

\(\eta_e\) = rendimento dell’elica

\(\eta_s\) = efficienza di scia = 1/(1 – w)

\(P_D\) = potenza erogata al mozzo dell’elica in CV

\(V\) = velocità della nave in nodi

La sollecitazione a compressione dovuta alla spinta dell’elica è

\(\sigma_c = {{S} \over A}\)

dove

\(A\) = area della sezione dell’asse portaelica

Quindi la sollecitazione ideale statica è

\(\sigma_{is} = \sqrt {{\sigma_c}^2 + 4 \cdot \tau^2}\)

Nella terza parte si parlerà delle sollecitazioni dinamiche che si sviluppano nell’albero portaelica, e poiché è importante il peso dell’elica si parlerà, anche, di un metodo di calcolo approssimativo del peso relativo all’elica.

Angelo Sinisi