Autonomia
L’autonomia, seconda parte: il rendimento propulsivo e l’elica isolata
Nella prima parte dell’articolo abbiamo parlato dell’equazione di R. Froude
\(\eta_d = \frac{P_E}{P_D}\) |
||||
dove |
\(\eta\) = è il rendimento che possiamo definire quasi-propulsivo (rendimento al mozzo) poiché manca il rendimento meccanico; |
|||
|
|
\(P_E\) = è la potenza effettiva richiesta dalla carena nelle prove di rimorchio; |
|||
|
|
\(P_D\) = è la potenza motrice sul mozzo dell’elica richiesta dalla carena in autopropulsione; |
|||
per cui il rendimento propulsivo è calcolato con la seguente formula
\(\eta_d = \eta_d \cdot \eta_{mecc}\) |
||||
dove |
\(\eta\) = è il rendimento propulsivo; |
|||
|
|
\(P_E\) = è il rendimento meccanico; |
|||
Nell’equazione di Froude il rendimento relativo rotativo \(\eta_r\) assume generalmente valori diversi dall’unità perché, alla condizione di identità di spinta, non corrisponde sempre la condizione di identità di potenza. Il valore del rendimento \(\eta_r\) risulta, quindi, tanto più lontano da uno quanto più, a parità di spinta fornita, il valore della potenza motrice richiesta dall’elica isolata differisce da quello della potenza motrice richiesta dall’elica unita allo scafo.
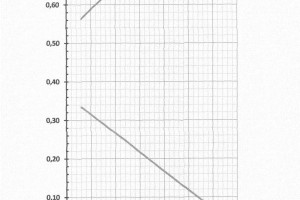
Nel caso in cui i detti due valori della potenza motrice coincidono, allora il rendimento relativo rotativo \(\eta_r\) risulta uguale all’unità. Poiché nel procedimento di analisi di Froude si ammette l’identità del numero di giri, sia il criterio d’identità di potenza che quello di spinta si possono trasformare rispettivamente in quelli di identità di coefficiente di spinta e di identità di coefficiente di momento. L’analisi, quindi, può essere effettuata in termini adimensionali mediante i diagrammi dell’elica isolata costituiti da un grafico (Figura 3) nel quale sull’asse delle ascisse è riportato il coefficiente d’avanzo
\(J= \frac{V_A}{( n \cdot D)}\) |
||||
dove |
\(V_A\) = velocità d’avanzo in m/sec |
|||
|
|
\(n\) = numero di giri al sec; |
|||
|
|
\(D\) = diametro dell’elica in m |
|||
e sull’asse delle ordinate sono riportati
|
|
a) i valori del coefficiente di spinta |
|||
\(K_T = \frac{T}{p \cdot D^2 \cdot n^2}\) |
||||
dove |
\(T\) = spinta in Kg |
|||
|
|
\(p\) = densità del fluido in \(Kg \cdot sec^2 / m^2\) |
|||
|
|
|
|||
|
|
b) i valori del coefficiente di coppia |
|||
\(K_Q= \frac{Q}{p \cdot D^5 \cdot n^2}\) |
||||
dove |
\(Q\) = coppia dell’elica, cioè il momento torcente in \(Kg \cdot m\) |
|||
|
|
|
|||
|
|
c) i valori del rendimento dell’elica |
|||
\(\eta_e = \frac{K_T}{K_Q}\cdot \frac{J}{2 \cdot \pi }\) |
||||
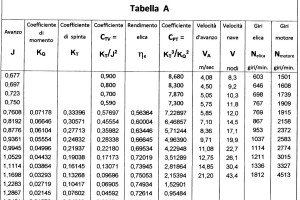
Tutti i suddetti valori, relativi all’elica isolata, sono riportati nella Tabella A. I diagrammi dell’elica isolata della Figura 3 definiscono il funzionamento dell’elica in tutto il campo che può interessare la propulsione.
Nella terza parte dell’articolo saranno calcolati la potenza assorbita dall’apparato motore.
Angelo Sinisi