Autonomia
L'autonomia, prima parte: la resistenza totale e il rendimento al mozzo
L’autonomia è la distanza che una nave può percorrere facendo assegnazione non solo sulle sue provviste di bordo, ma anche, in modo particolare, sul combustibile disponibile per la propulsione.
Per un’auto l’autonomia è stabilita dalla quantità di carburante che il serbatoio può contenere e sulle autostrade è circa 8÷10 volte la distanza che intercorre tra due distributori. Quindi per il conducente, secondo la distanza che deve percorrere, si deve fermare più o meno volte per riempire il serbatoio. Nel caso estremo, se dovesse cioè consumare tutto il combustibile prima di arrivare ad un distributore, ha molti modi per procurarsi il combustibile e la sua vita certamente non è in pericolo.
Tutto quello che abbiamo detto per l’auto non vale però per una nave o imbarcazione che sia, perché rimanere in mare senza combustibile vuol dire rimanere in balia delle onde, si va alla deriva. Questa condizione è pericolosissima perché, secondo le condizioni del mare, si può arrivare al capovolgimento del natante, mettendo quindi in pericolo la vita stessa dei passeggeri.
Ecco perchè l’autonomia è un elemento importante che viene sempre definito nel progetto operativo di una nave. Cioè in fase di progetto, non solo deve essere definita l’autonomia alla velocità di crociera, ma a tutte le velocità da zero alla velocità massima raggiungibile. Questo permette al comandante del natante di sapere quale velocità gli consente di percorrere la distanza maggiore.
Normalmente l’autonomia in miglia marine alla velocità di crociera è calcolata con la seguente formula
\(\frac{lt}{(\frac{gr/CV \cdot h}{Y}) \cdot P_A} \cdot V =\) miglia di autonomia |
||||
dove |
\(lt\) = litri totali del combustibile disponibile per la propulsione |
|||
|
|
\(gr/CV \cdot h\) = consumo orario in grammi per cavallo potenza ora del motore |
|||
|
|
\(Y\) = peso specifico del combustibile |
|||
|
|
\(P_A\) = potenza motore in cavalli ottenuta dividendo la potenza effettiva \(P_E\) per il rendimento propulsivo totale \(\eta_P\), fissato in modo cautelativo |
|||
|
|
\(V\) = velocità in nodi della nave |
|||
Con lo stesso sistema possiamo tracciare la curva dell’autonomia nel campo di velocità che va dallo zero alla massima velocità. Ma, come abbiamo detto, questo valore dell’autonomia non è sufficiente e, per poter proseguire nello sviluppo dell’analisi del problema, utilizziamo i dati di una carena planante
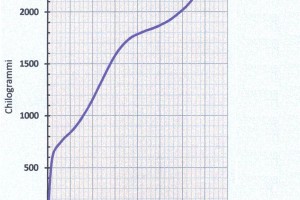
Di questa carena conosciamo la resistenza d’onda, la resistenza di attrito, la resistenza di attrito degli spruzzi, la resistenza del vento e la resistenza delle appendici. Per cui la resistenza totale in chilogrammi (Figura 1) sarà
\(R_T = R_R + R_F + R_{F_S}+ R_V + R_{app}\)
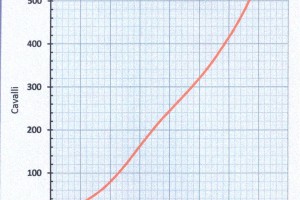
e la potenza effettiva (Figura 2) sarà
\(P_E= \frac{0,51444 \cdot R_T \cdot V}{75}\)
La potenza dell’apparato motore, considerando un rendimento propulsivo costante, sarà
\(P_A = P_E/ \eta_p \)
Il confronto del funzionamento dell’elica unita alla carena con il funzionamento dell’elica isolata viene basato sulla ipotesi che, a parità di numero di giri, i valori del rendimento dell’elica e della sua velocità d’avanzo, nelle due condizioni di funzionamento considerate, siano uguali quando si ha identità della spinta fornita dall’elica. Questo criterio di analisi fu proposto da R. Froude nel 1883 insieme alla nota equazione che coordina gli elementi che, separatamente, si deducono dalle prove di rimorchio della carena, dalle prove dell’elica isolata e dalle prove di autopropulsione.
L’equazione di R. Froude è la seguente:
\(\eta_d = \frac{P_E}{P_D}= \frac{1-t}{1-w} \cdot \eta_e \cdot \eta_r\) |
||||
dove |
\(\eta_d \) = è il rendimento che possiamo definire quasi-propulsivo (rendimento al mozzo) poiché manca il rendimento meccanico; |
|||
|
|
\(P_E\) = è la potenza effettiva richiesta dalla carena nelle prove di rimorchio; |
|||
|
|
\(P_D\) = è la potenza motrice sul mozzo dell’elica richiesta dalla carena in autopropulsione; |
|||
|
|
\((1-t)\) = R/S è il rapporto fra la resistenza \(R\) della carena a rimorchio e la spinta \(S\) che si ha sull’asse dell’elica in autopropulsione ed è definito come “coefficiente di risucchio”; |
|||
|
|
\((1-w)\) = \(V_A/V\) dove \(V_A\) è la velocità d’avanzo che si ha per l’elica isolata allo stesso numero di giri ed allo stesso valore di spinta \(S\) e \(V\) è la velocità della carena nelle prove di rimorchio e di autopropulsione ed è definito come “coefficiente di scia”; |
|||
|
|
\(\eta_e\) = è il rendimento dell’elica isolata a parità di numero di giri e di spinta; |
|||
|
|
\(\eta_r\) = è un fattore numerico detto “rendimento relativo rotativo”, che serve a stabilire l’eguaglianza aritmetica fra i due membri dell’equazione di Froude. |
|||
Nella seconda parte parleremo del rendimento propulsivo e dell’elica isolata.
Angelo Sinisi