La stabilità delle navi: baricentro, centro di carena e momento statico

Questa è la prima parte dell’articolo composto di quattro parti. Negli articoli precedenti, relativi alla progettazione di una carena, ho accennato all’altezza metacentrica (r – a) (indice di stabilità) (Figura 1) come valore importante per la stabilità trasversale che va ricercato attraverso corrette proporzioni di scafo. In quest’articolo cercherò di spiegare in modo più approfondito il concetto e le condizioni di stabilità dell’equilibrio delle navi.

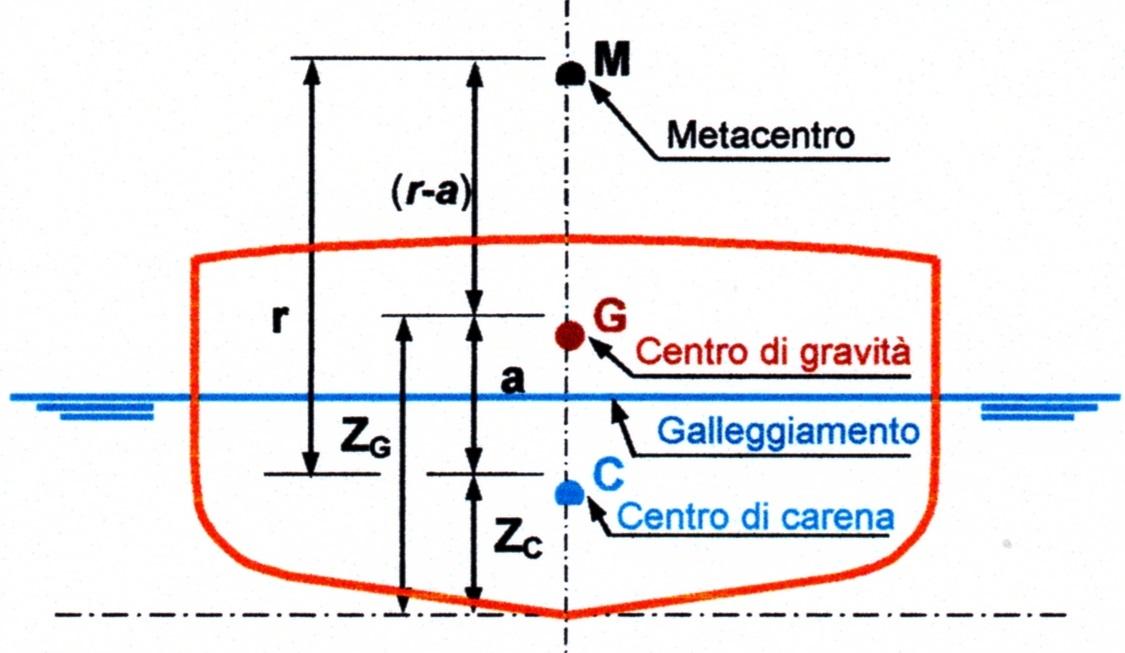
Per capire meglio il suddetto concetto è necessario comprendere il significato di: il baricentro o centro di gravità, il centro di carena, il momento statico, il momento d’inerzia, la forza.

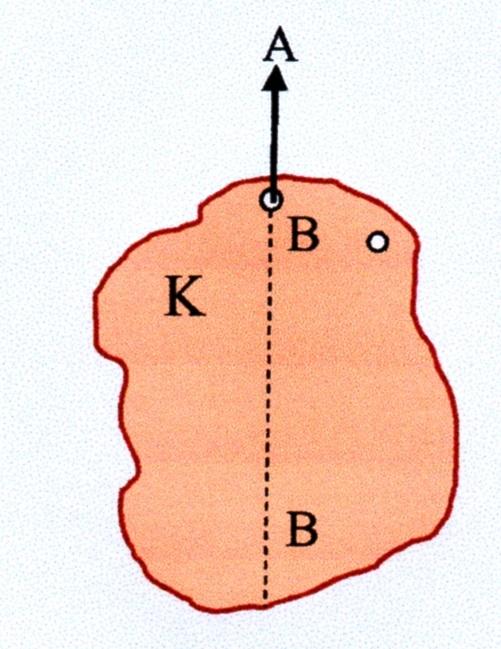
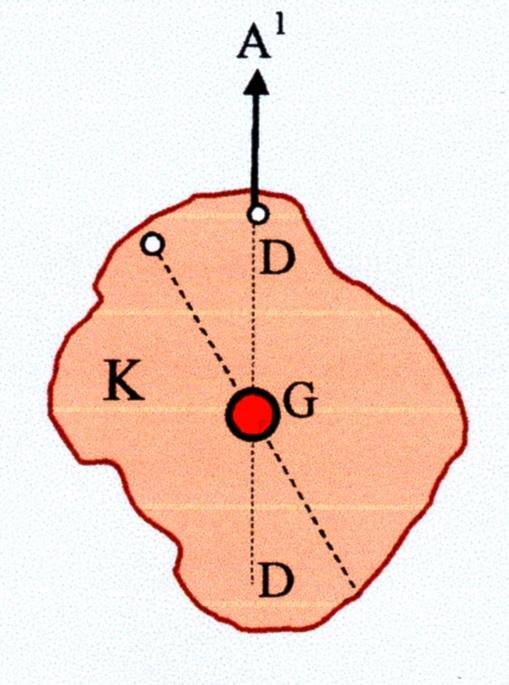
a) Il “baricentro di un corpo” è il punto in cui può essere concentrata la massa del corpo stesso. Il baricentro di un corpo si definisce anche “centro di gravità G”. Se il corpo ha un asse di simmetria, il baricentro o centro di gravità G appartiene a tale asse. Se teniamo sospeso, prima, un corpo K (Figura 2) dal punto B con una corda A e tracciamo una retta tratteggiata B-B secondo la direzione della corda, possiamo dire che il centro di gravità si trova su questa retta tratteggiata. Dopo sospendiamo lo stesso corpo K con una corda A¹ (Figura 3) per il punto D e tracciamo una retta tratteggiata D-D che, secondo la direzione della corda, incrocia la retta B-B nel punto G. Tale punto è il centro di gravità.

b) Il “centro di carena” è il baricentro del volume dell’opera viva della carena, cioè il volume della carena che si trova sotto il galleggiamento. Si potrebbe definire il centro di carena anche come il centro di gravità della massa fluida spostata dalla nave. Per questo centro passa la retta lungo la quale agisce la spinta di Archimede. Il principio di Archimede, vissuto nel terzo secolo avanti Cristo, afferma che un corpo immerso in un fluido riceve una spinta verticale, dal basso verso l’alto, d’intensità uguale al peso di una massa di fluido di forma e volume uguale a quella della parte immersa del corpo.

Se un corpo di peso P (Figura 4) con la forma di un prisma regolare, immerso in un fluido, ha una immersione pari a Z si ha che la spinta \(S_P\) sarà

\(S_P=∇_f \cdot \rho\)

dove

\(S_P\) = Spinta
\(∇_f \) = volume del fluido spostato
\(\rho\) = densità del fluido

per cui

\(S_P=∇_f \cdot \rho = P\)

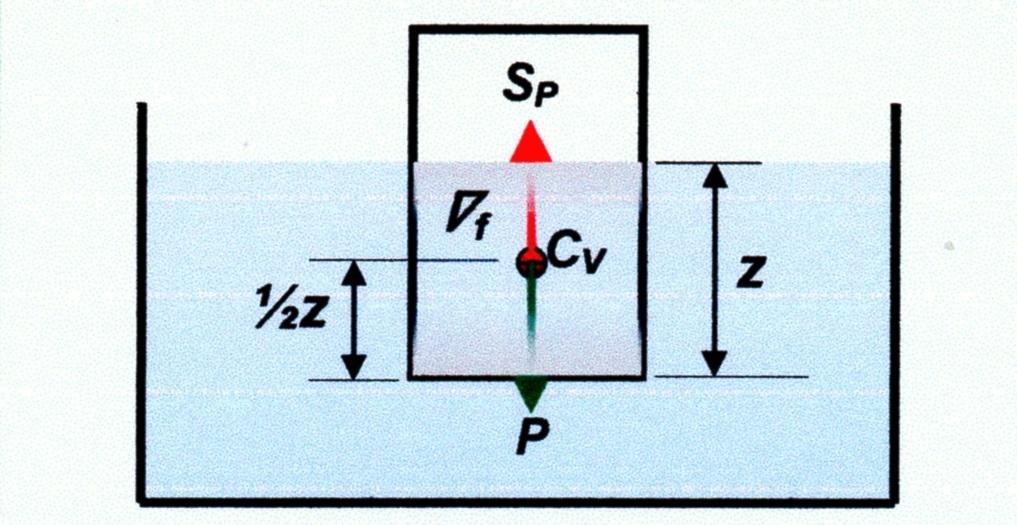
La direzione della spinta \(S_P\) opposta a quella del peso P passeranno per il punto \(C_V\) che è il centro del volume o il baricentro del fluido spostato.

c) Data una retta \(n\) (Figura 5) nel piano delle masse e misurate le distanze \(d_i\), secondo una prefissata direzione \(y\) , si definisce come “momento statico” di un sistema di masse rispetto all’asse \(n\) la somma dei prodotti delle masse per le relative distanze dall’asse \(n\) , per cui

\(M_S=∑(m_i \cdot d_i)\)

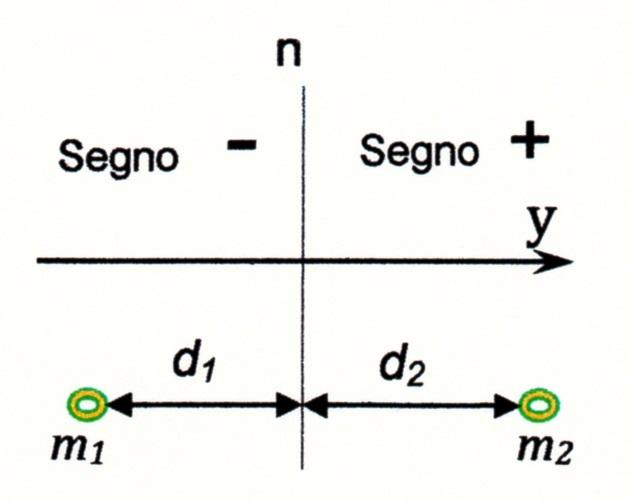
Il momento statico può risultare positivo, negativo o nullo poiché, anche nel caso in cui tutte le masse siano positive, ogni termine della somma ha il segno dipendente dalla distanza che può essere negativa o positiva a seconda che la massa si trovi da una parte o dall’altra della retta \(n\) .

Se nella Figura 5

\(m_1=m_2\) e \(d_1=d_2\)

sarà \(- m_1d_1 + m_2d_2=0\)

e la retta \(n\) passa sicuramente per il baricentro del sistema di masse.

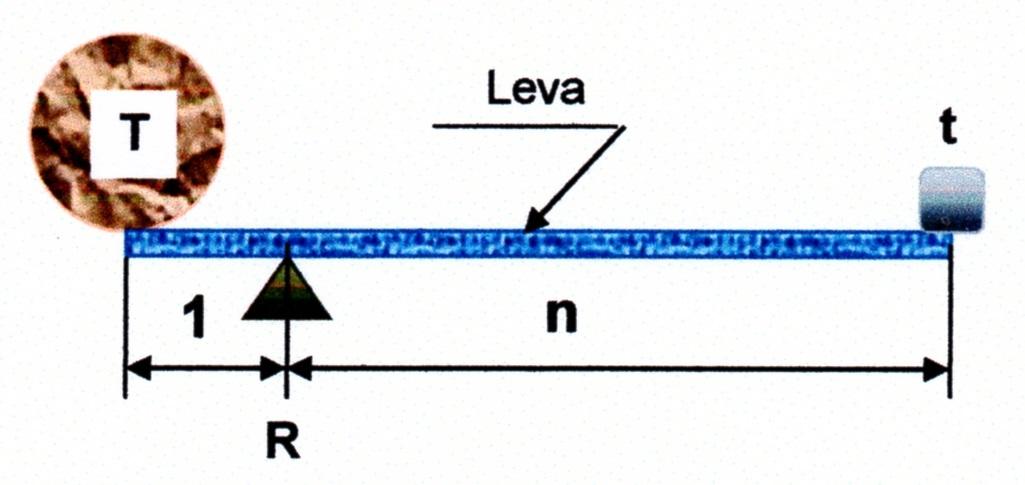
Quindi il momento statico è utile per trovare il baricentro di un sistema di masse e inoltre può aiutarci a capire la frase di Archimede “datemi una leva abbastanza lunga (aggiungo: e robusta) e un punto di appoggio, e vi solleverò il mondo” (Figura 6).

Nella seconda parte dell’articolo sarà sviluppato il concetto del momento d’inerzia e della forza.

Angelo Sinisi