Autonomia
L'autonomia, quarta parte: il rendimento propulsivo totale variabile
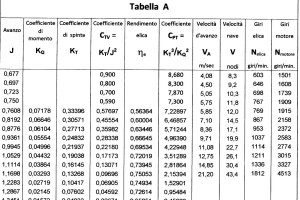
Il valore del coefficiente \(C_{TV}= K_T /J^2\) della Tabella B, che prescinde dal valore dei giri dell’elica alle varie velocità, si ottiene eguagliando l’espressione dei numeri di giri che si ricavano dal coefficiente di spinta \(K_T\) e da quelli del coefficiente d’avanzo J. Infatti
|
|
\(K_T = \frac{T}{p \cdot D^4 \cdot n^2};\) \(n^2 = \frac{T}{104,61 \cdot D^4 \cdot K_T} \) |
|||
elevando al quadrato l’espressione dell’avanzo si ha
|
|
\(J = \frac{V_A}{n \cdot D};\) \(n^2 = \frac{V^2_A}{D^2 \cdot J^2}\) |
|||||
|
|
per cui |
\(\frac{T}{104,61 \cdot D^4 \cdot K_T} = \frac{V^2_A}{D^2 \cdot J^2};\) \(\frac{K_T}{J^2}= \frac{T}{104,61 \cdot D^2 \cdot V^2_A}\) |
|
|||
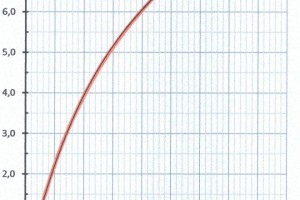
Mettendo in curva i valori, che sono nella Tabella A, di \(C_{PT} = K^3_T/K^2_Q\) in funzione di \(C_{TV} = K_T/J^2\), ricavati dai valori dell’elica isolata, nel grafico della Figura 7 con un piccola estrapolazione in modo da poter ricavare, interpolando, i valori del coefficiente \(C_{PT}\) in funzione del coefficiente \(C_{TV}\) della Tabella B.
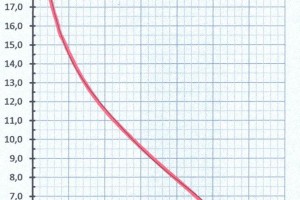
Ponendo in curva i valori, che sono nella Tabella B, della velocità d’avanzo \(V_A\) in funzione del coefficiente \(C_{PT}= K^3_T/ K^2_Q\) nel grafico della Figura 8 in modo da poter ricavare, interpolando, i valori della velocità d’avanzo \(V_A\) in funzione del coefficiente \(C_{PT}= K^3_T/ K^2_Q\) della Tabella A. Nella Tabella A poiché i giri al minuto primo N si ricavano dalla seguente formula, si ha
|
|
\(N_{elica}= \frac{V_A}{J \cdot D} \cdot 60\) |
|||
La riduzione dei giri dell’elica rispetto a quelli del motore è di 2,49, si ha che i giri del motore saranno
|
|
\(N_{motore}= N_{elica} \cdot 2,49\) |
|||
Ora abbiamo tutti gli elementi per calcolare la potenza al mozzo \(P_D\), la potenza motore totale assorbita dalle eliche alle varie velocità e quindi il rendimento propulsivo \(\eta_p\) alle varie velocità. Come abbiamo già visto il coefficiente di spinta e il coefficiente di coppia sono
|
|
\(K_T= \frac{T}{p \cdot D^4 \cdot n^2};\) \(K_Q= \frac{Q}{p \cdot D^5 \cdot n^2};\) |
|||||
|
|
da cui si ricava che |
\(Q= \frac{75 \cdot P_D}{N \cdot 2 \cdot \pi}= \frac{716,197 \cdot P_D}{60 \cdot n}=11,937 \cdot \frac{P_D}{n}\) |
|
|||
|
|
per cui |
\(K_Q= \frac{11,937 \cdot \frac{PD}{n}}{104,61 \cdot D^5 \cdot n^2}= \frac{0,11411 \cdot P_D}{D^5 \cdot n^2}\) |
|
|||
essendo il coefficiente \(C_{PT}= K^3_T/K^2_Q\) si ha
|
|
|
\(\frac{K^3_T}{K^2_Q}= \frac{\frac{T^3}{p^3 \cdot D^{12} \cdot n^6}}{ \frac{0,11411^2 \cdot P^2_D}{D^{10} \cdot n^6}}= \frac{T^3}{p^3 \cdot D^{12} \cdot n^6} \cdot \frac{D^{10}\cdot n^6}{0,11411^2 \cdot P^2_D}= \frac{T^3}{14906,2 \cdot D^2 \cdot P^2_D}\) |
|
|||
|
|
quindi si avrà |
\(P_D = \begin{bmatrix} \frac{T^3}{\frac{K^3_T}{K^2_Q} \cdot 14906,2 \cdot D^2} \end{bmatrix}^{0,5}= \frac{1}{122,091 \cdot D} \cdot \sqrt{\frac{T^3}{(\frac{K^3_T}{K^2Q})}}\) |
|
|||
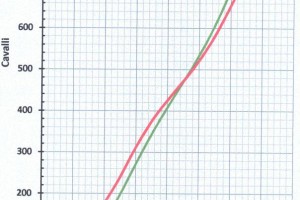
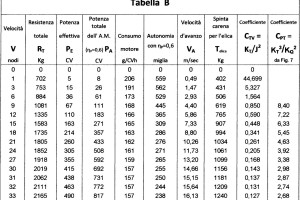
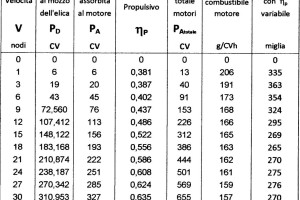
Nella suddetta formula i valori della spinta \(T\) e del coefficiente \(C_{PT}\) sono quelli indicati nella Tabella B e i valori della potenza al mozzo \(P_D\) che sono nella Tabella C sono tracciati nella Figura 9. Avuti i valori di \(P_D\) possiamo ricavare la potenza totale \(P_A\) dei motori, che possiamo sovrapporre nella Figura 4 a quella tracciata con rendimento propulsivo \(\eta_P\) costante e possiamo notare le differenze dell’andamento delle curve. Nella curva con rendimento propulsivo \(\eta_P\) variabile si nota, in modo evidente, come cambia l’andamento della curva nella zona di planata.
Nella Tabella C possiamo calcolare il rendimento propulsivo \(\eta_P= P_E/ P_A\) da dove si evince con chiarezza la differenza che i valori del rendimento propulsivo \(\eta_P\) hanno alle varie velocità.
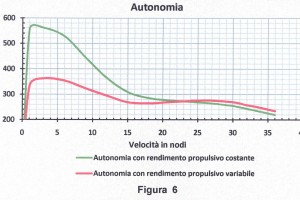
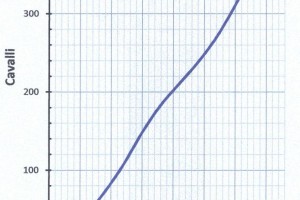
Conosciuta la potenza totale \(P_A\) dei motori alle varie velocità possiamo ricavare la curva dell’autonomia con rendimento propulsivo \(\eta_P\) variabile nella Figura 6. E’ evidente la differenza delle due curve dell’autonomia, sia nella quantità di miglia che nell’andamento. L’autonomia con rendimento \(\eta_P\) variabile mette in evidenza la zona critica dei consumi tra i 14 e i 23 nodi. In modo particolare alle basse velocità l’autonomia con rendimento \(\eta_P\) variabile diminuisce di circa il 60% rispetto a quella con rendimento propulsivo \(\eta_P\) costante.
Spero di essere stato esauriente nel dimostrare quanto sia importante conoscere la curva vera dell’autonomia per il comandante di una imbarcazione, grande o piccola che sia, e quindi poterla determinare in fase di progetto in modo tale da soddisfare il progetto operativo.
Angelo Sinisi