Autonomia
L’autonomia, terza parte: la potenza dell’apparato motore
Dopo aver realizzato, nella seconda parte, il grafico dell’elica isolata in questa terza parte dell’articolo verranno calcolati tutti gli elementi necessari per ottenere la potenza dell’apparato motore. I primi elementi necessari sono la frazione di scia e la frazione di riduzione di spinta
\(w = \frac{V - V_A}{V}\) |
||||
e \(t= \frac{T-R_T}{T}\) |
||||
dove |
\(V\) = velocità della nave |
|||
|
|
\(V_A\) = velocità di avanzo |
|||
|
|
\(T\) = spinta dell’elica |
|||
|
|
\(R_T\) = resistenza totale della nave |
|||
|
|
|
|||
|
|
Utilizzando le seguenti formule di Holtrop si ha |
|||
\(w= 0,3095 \cdot C_B + 10 \cdot C_V \cdot C_B - 0,23 \cdot \frac{D}{\sqrt{B_{WL} \cdot T_{WL}}}\) |
||||
dove |
\(D\) = diametro dell’elica |
|||
|
|
\(B_{WL}\) = larghezza al galleggiamento |
|||
|
|
\(T_{WL}\)= immersione |
|||
|
|
\(C_B\)= coefficiente di blocco |
|||
|
|
\(C_V\)= coefficiente di resistenza viscosa = \(= (1 + k) \cdot C_F + C_A\) |
|||
|
|
|
|||
\(C_A = \begin{bmatrix} 105 \cdot (\frac{K_S}{L_{WL}})^{\frac{1}{3}} - 0,64 \end{bmatrix} \cdot 10^{-3} \)\(K_S = 150 \cdot 10^{-6} \) |
||||
dove |
\(L_{WL}\) = lunghezza al galleggiamento |
|||
|
|
\(C_F\) = coefficiente di resistenza d’attrito |
|||
|
|
\((1+k)\)= fattore di forma determinato dalle prove di resistenza in vasca |
|||
|
|
\(K_S\)= \(150 \cdot 10^{-6} m\) |
|||
|
|
||||
\(t = 0,325 \cdot C_B - -0,1885 \cdot \frac{D}{\sqrt{B_{WL} \cdot T_{WL}}}\)
|
||||
Possiamo fissare l’efficienza di risucchio \((1-t)= 0,9\)e il fattore di scia \((1 -w) = 0,95\), considerando il buon rendimento dell’elica isolata \(\eta_e =0,73 \) , il rendimento relativo rotativo \(\eta_e =0,73 \), il rendimento meccanico \(\eta_{mecc} =0,95 \) e l’inclinazione della linea d’asse si può calcolare il rendimento propulsivo \(\eta_e =0,6\).
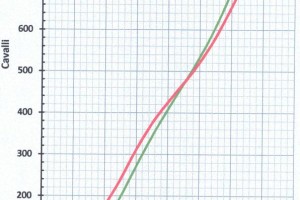
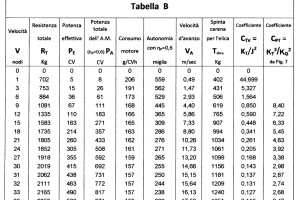
Ora possiamo calcolare la potenza assorbita dall’apparato motore \(P_A\) con il rendimento propulsivo costante \(\eta_e =0,6\) (Figura 4 e Tabella B).
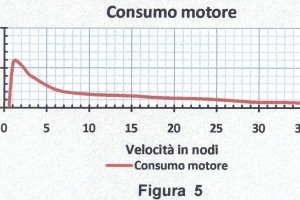
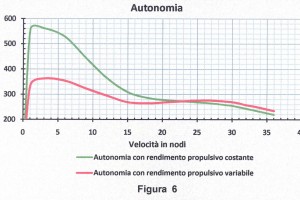
Stabilita la quantità di litri 1100 del combustibile, consumabile per la propulsione, e conoscendo il consumo del motore (Figura 5 e Tabella B) alle varie velocità possiamo calcolare l’autonomia alle varie velocità (Figura 6) con la seguente espressione
|
|
Autonomia in miglia = \(\frac{lt}{(\frac{gr/CV \cdot h}{Y}) \cdot P_A} \cdot V = \frac{1100 \cdot 840 \cdot V}{(gr/ CV \cdot h) \cdot P_A} = \frac{924000 \cdot V}{(gr / CV \cdot h) \cdot P_A}\) |
|||
Calcoliamo la velocità d’avanzo e la spinta richiesta dalla carena per un’elica nella Tabella B con le seguenti formule
|
|
\(V_A = V \cdot (1 - w) \) e \(T_{carena} = R_T/(1-t)\) |
|||
Poiché vi sono due linee d’assi, la spinta \(T_{elica}\) è calcolata considerando anche l’inclinazione della linea d’asse, per cui si ha
|
|
\(T_{elica}= R_T/((1-t)\cdot (2 \cdot 0,97))\) |
|||
Nella quarta ed ultima parte verrà calcolato il rendimento propulsivo totale e variabile a tutte le velocità, in modo da ottenere un’autonomia il più veritiera possibile.
Angelo Sinisi