
La carena a spigolo o planante - quarta parte
Prosegue l'approfondimento sulla carena a spigolo o planante ed in particolare su tutti gli aspetti che contribuiscono a formare la resistenza totale della carena
Per uno scafo planante il calcolo della resistenza di attrito \(R_F\) è uguale a quello che viene eseguito per le navi dislocanti. Tuttavia, contrariamente a quanto avviene per le navi a dislocamento, la resistenza di attrito \(R_F \) alle velocità di planata, avendo valore più elevato rispetto alla resistenza residua \(R_R\) , diviene, quanto più alta è la velocità, il componente predominante della resistenza totale.

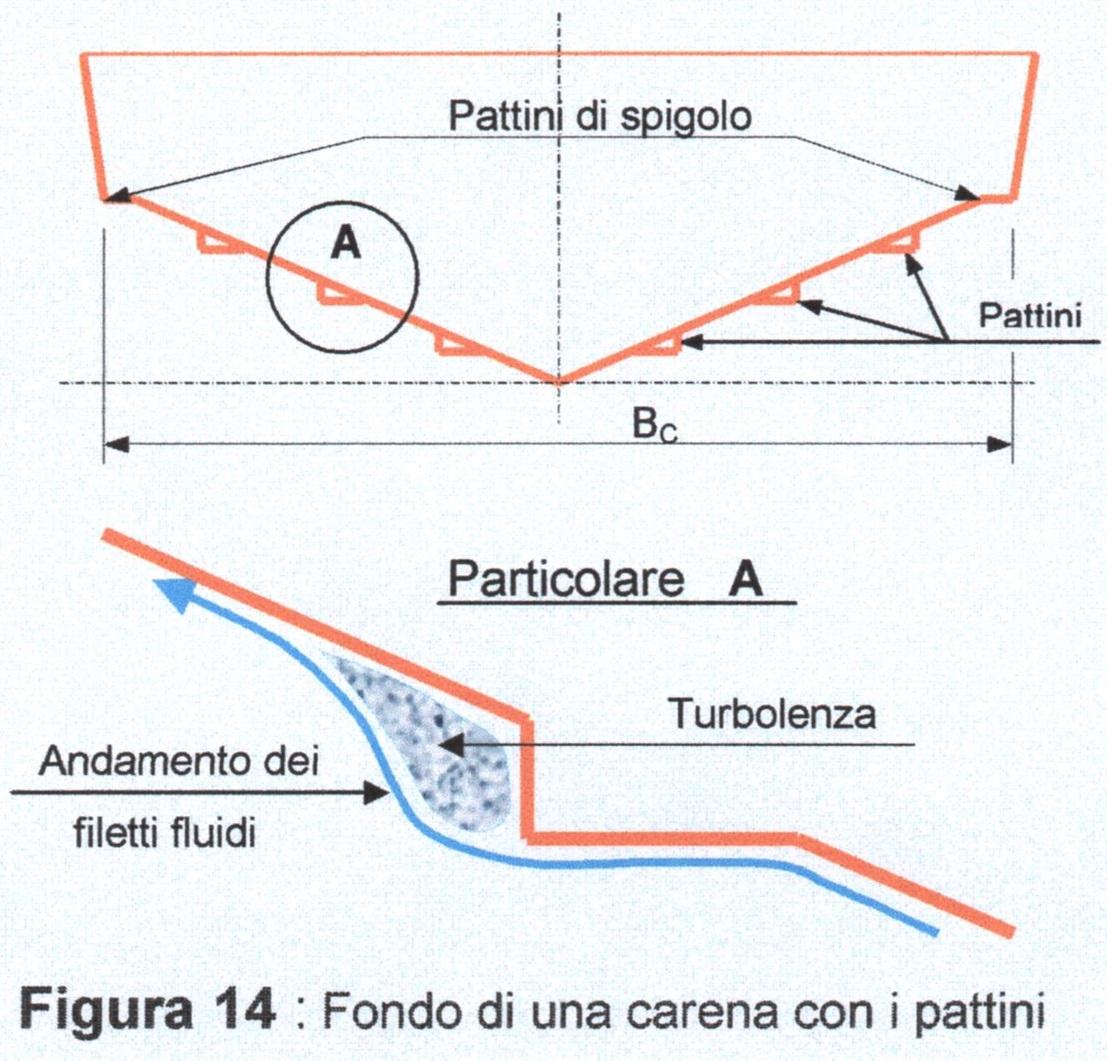
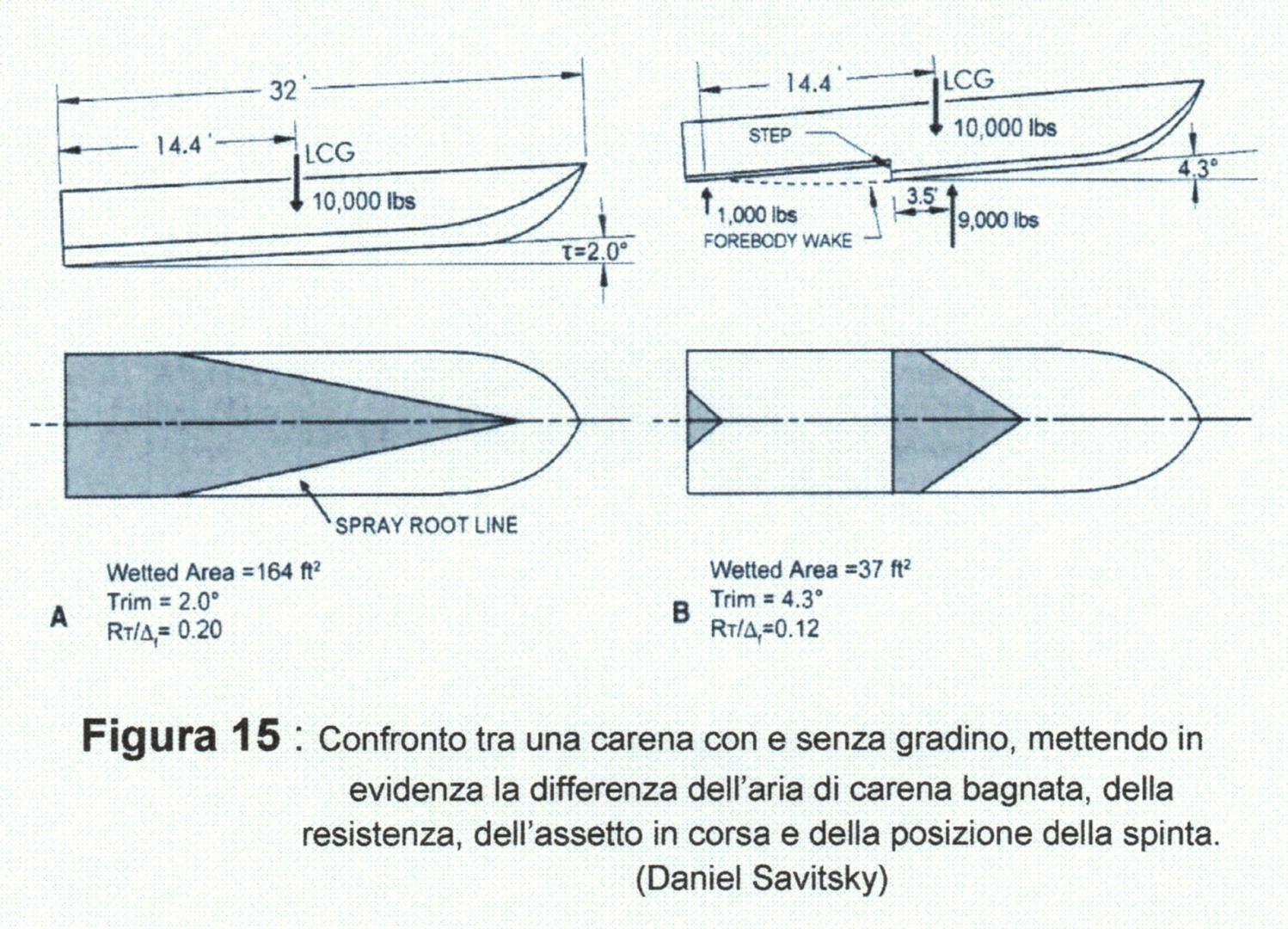
Infatti, questo spiega il perché deve essere fatto il possibile per renderla più piccola e il perché si usano i pattini (Figura 14), e talvolta si ricorra allo scafo a gradino (Figura 15), per mezzo dei quali si riduce la superficie bagnata, creando anche uno strato di turbolenza di aria e acqua che funge da lubrificante per il fondo. Questo fenomeno di turbolenza di aria e acqua si nota con chiarezza nella Figura 1.
Inoltre nella Figura 15 si nota la differenza della figura bagnata del fondo senza gradino e con gradino, evidenziando il diverso assetto longitudinale e la diversa distribuzione della spinta.
Per il calcolo della resistenza di attrito \(R_F\) si ha
\(R_F = C_F \cdot(\rho/2) \cdot A \cdot V^2\) |
|||
dove |
\(R_F=\) resistenza di attrito |
||
|
|
\(C_F\) = coefficiente di attrito |
||
|
|
\(\rho\) = densità dell’acqua di mare |
||
|
|
\(A\) = superficie bagnata della carena |
||
|
|
\(V\) = velocità dello scafo |
||
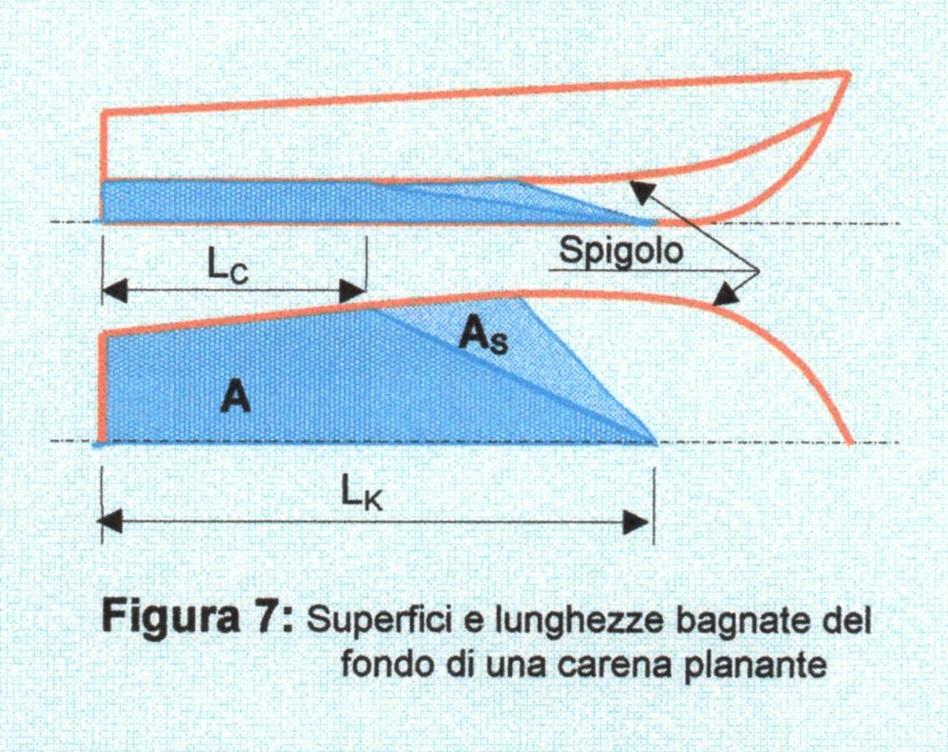
Per risolvere la suddetta equazione è necessario trovare con una buona approssimazione la superficie bagnata del fondo della carena alle varie velocità e conseguentemente la lunghezza bagnata in chiglia \(L_K\) e allo spigolo \(L_C\) (Figura 7).
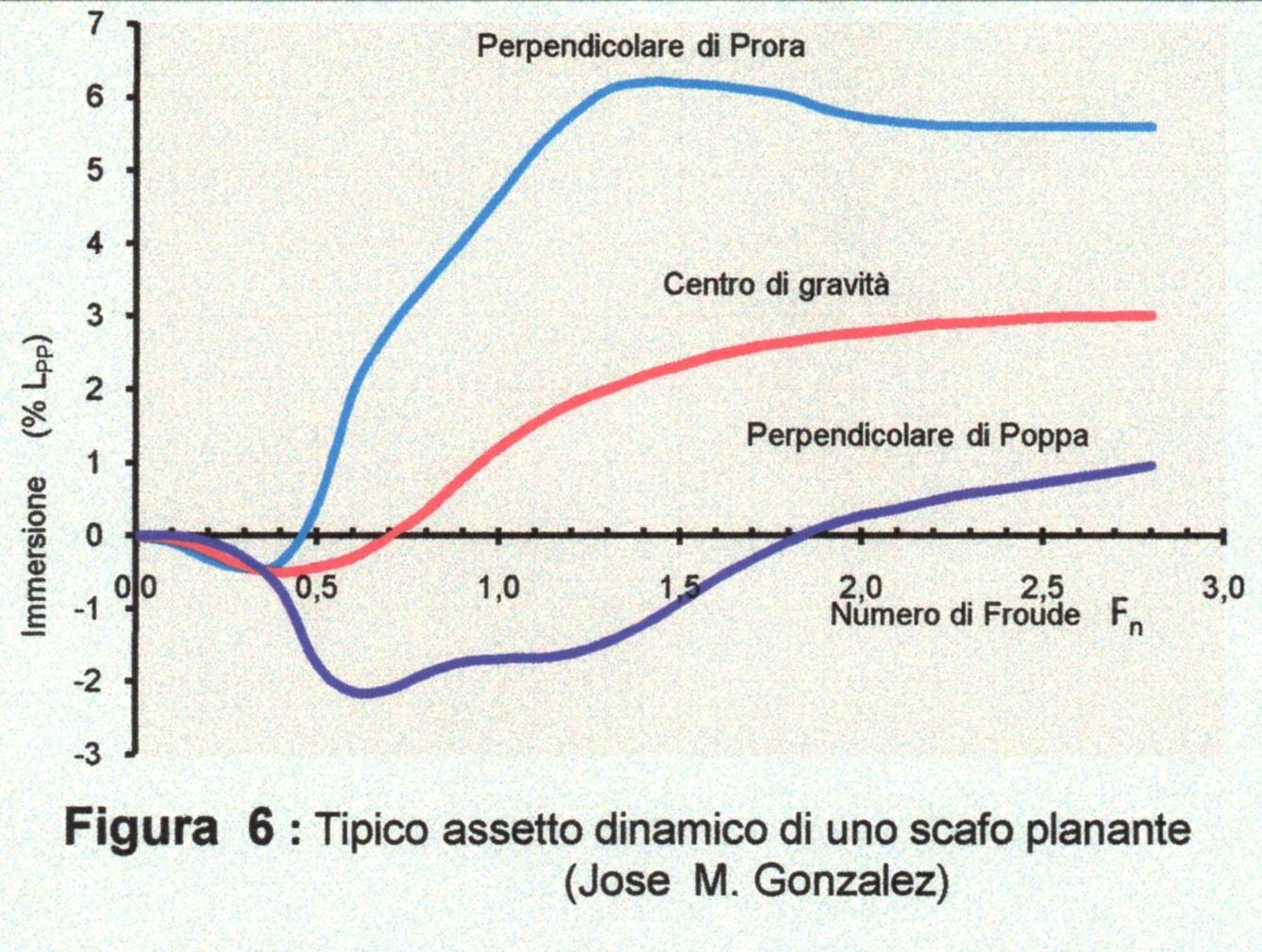
Man mano che la velocità aumenta la carena esce sempre di più dall’acqua (Figura 6) e la superficie bagnata si riduce sempre di più rispetto al valore che aveva a scafo fermo. La Figura 6 rende comprensibile in modo evidente quanto detto mettendo in evidenza la posizione verticale del centro di gravità, dell’immersione di prora e dell’immersione di poppa alle varie velocità, in funzione del numero di Froude \(F_n=(V/\sqrt{g \cdot L_{WL}})\). Infatti, per \(0<F_n <0,5\), date le forme di una carena planante, si formano degli effetti di depressione che affossano nell’acqua l’imbarcazione.
Dopo \(F_n= 0,5\) l’imbarcazione si appoppa per effetto della spinta dinamica raggiungendo la massima immersione della poppa. Aumentando la velocità e raggiunto il punto \(F_n ≂ 1,3\) si ha il massimo angolo di assetto in corsa ed è il punto in cui, avendo riserva di potenza, si supera la gobba di resistenza e l’imbarcazione, aumentando la velocità, riduce sempre di più l’angolo di assetto in corsa fino a raggiungere un equilibrio dinamico per \(F_n ≳ 2,1\) .
Per quanto detto in precedenza, cioè che la resistenza d’attrito \(R_F\) alle alta velocità è il componente principale della resistenza totale \(R_T\) di uno scafo planante, la superficie bagnata e la lunghezza bagnata in corsa diventano fattori importantissimi del progetto. Un cambiamento d’assetto anche se piccolo porta a variazioni della lunghezza in chiglia \(L_K\) della superficie bagnata \(A\) e quindi della resistenza di attrito \(R_F\).
Come abbiamo già detto, la larghezza fra gli spigoli \(B_C\) (Figura 14) è molto importante per la stabilità statica, dinamica e resistenza, sia per superare la gobba sia per la velocità massima. La stabilità statica si ricava con stesso metodo usato per le carene tonde, già definito nell’articolo precedente.
Il calcolo seguente sarà ripetuto tante volte per quanti valori della larghezza \(B_C\) vogliamo fissare per il campo di velocità che vogliamo esaminare. Quindi, dopo aver calcolato l’esponente di carico con la posizione longitudinale e verticale del centro di gravità, possiamo fissare con certezza i seguenti valori
\(1)\Delta\) |
= dislocamento |
|
\(2) B_C\) |
= larghezza agli spigoli |
|
\(3) V\) |
= velocità dello scafo |
|
\(4) X_G\) |
= ascissa del centro di gravità |
|
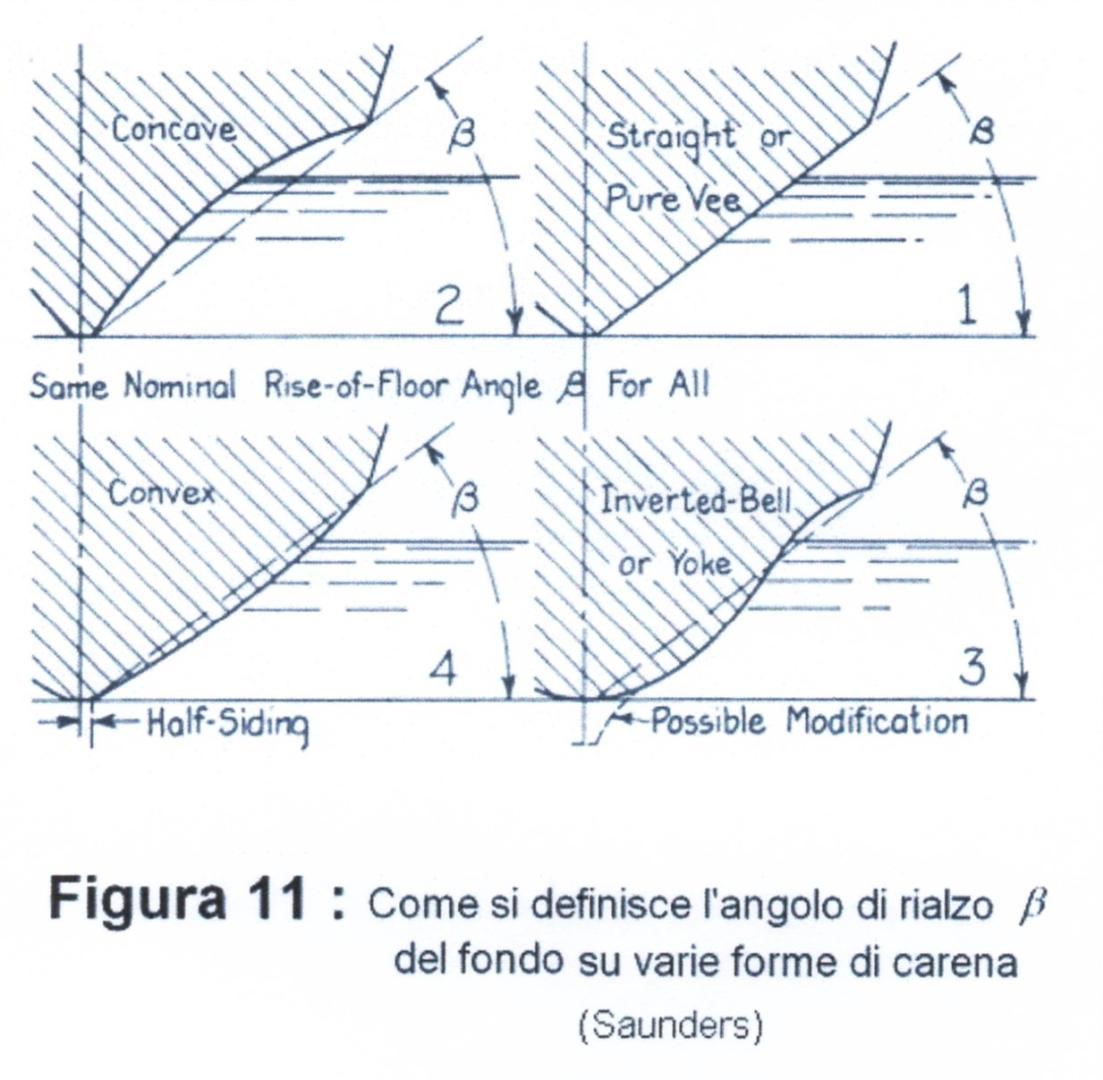
\(5) \beta\) |
= angolo di rialzo del fondo dello scafo (Figura 11) |
Conosciuti i valori precedentemente indicati possiamo calcolare il coefficiente di velocità \(C_V\) e il coefficiente di peso \(C_\Delta\).
| \(C_V=V/\sqrt{{g \cdot B_C}};\) | \(C_\Delta= \Delta/(\rho\cdot g \cdot B_C^3)\) |
| poichè \(\rho= \gamma / g\) | possiamo semplificare \(C_\Delta= \nabla/ B_C^3\) |
| dove | \(C_\Delta= \) coefficiente di peso |
| \(C_V=\) coefficiente di velocità | |
| \(\Delta =\) volume | |
| \(g =\) coefficiente di velocità | |
| \(\gamma=\) peso specifico | |
| \(\rho= \) densità dell’acqua di mare |
Abbiamo tutti i dati per calcolare il coefficiente di portanza relativo alla carena con angolo di rialzo \(\beta\), per cui
\(C_{L\beta}= \Delta /(0,5 \cdot \rho \cdot V^2 \cdot B_C^2) = (2 \cdot C_ \Delta ) /C_V^2\)
il coefficiente \(C_{L\beta}\) in funzione del coefficiente di portanza relativo con \(\beta =0\) è
\(C_{L\beta}=C_{L0} -0,0065 \cdot \beta \cdot C_{L0}^{0,6}\)
da cui si ricava il coefficiente di portanza \(C_{L0}\). La posizione del punto di applicazione della pressione o portanza è
\(L_p=X_G= \lambda\cdot B_C \cdot (0,75 - 1/(5,21 \cdot(C_V^2/\lambda^2)+2,39))\) |
|||
| Dove | \(\lambda\) = rapporto di figura | ||
| \(L_P\)= ascissa del punto di applicazione della pressione | |||
| \(C_V\)= coefficiente di velocità | |||
da cui possiamo ricavare il rapporto di figura \(\lambda\) , che è uguale a \(\lambda= L_K + L_C/(2 \cdot B_C)\)
| poichè \(L_m= (L_K + L_C)/2\) | si ha \(\lambda = L_m/B_C\) |
| dove | \(L_K= \) lunghezza bagnata in chiglia |
| \(L_C=\) lunghezza bagnata allo spigolo |
da cui la lunghezza media della figura bagnata sotto carena è \(L_m=\lambda \cdot B_C \)
Il coefficiente di portanza per β=0 si può risolvere anche con la seguente equazione
\(C_{L0}=\theta^{1.1} \cdot (0,12 \cdot \sqrt{\lambda}+((0,00055\cdot \lambda^{2,59})/C_V^29))\)
Conoscendo \(C_{L0}\) e \(\lambda\) possiamo ricavare il valore dell’angolo di assetto longitudinale o trim \(\theta\) . La lunghezza bagnata in chiglia è data dalla seguente formula
\(L_K= B_C \cdot (\lambda + (tan \beta/(2 \cdot \pi \cdot tan\theta)))\) |
|||
| Dove | \(B_C\) = larghezza agli spigoli | ||
| \(\lambda\)= rapporto di figura | |||
| \(\beta\)= angolo di rialzo del fondo dello scafo | |||
| \(\theta\)= angolo di assetto in corsa | |||
Ora abbiamo tutti gli elementi per calcolare la superficie bagnata, la resistenza di attrito e tutte le altre resistenze che contribuiscono a formare la resistenza totale della carena. Argomenti che saranno sviluppati nella prossima parte dell’articolo.








