La carena a spigolo o planante - terza parte

L’equilibrio in corsa e la resistenza d’onda

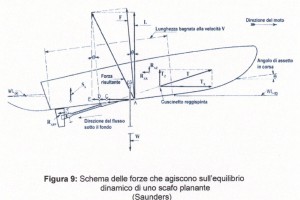
Dalle parti precedenti di questo articolo, già pubblicate, si evince che uno scafo a spigolo quando plana si trova in un equilibrio dinamico, determinato dalle forze in gioco (Figura 9). Dalle condizioni di equilibrio per le suddette forze, otteniamo, per le sole componenti orizzontali, che la resistenza totale al rimorchio è data da

\(R_t=L \cdot tan \theta +\frac{(R_f+ R_{APP})}{cos \theta}+R_{AX}\)

per l’equilibrio verticale si ha

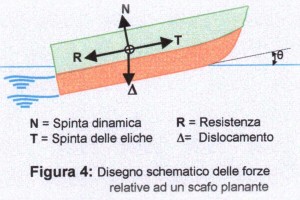
Mettere d’accordo tutte queste forze è arduo. Quando lo scafo è a regime, si deve avere, ovviamente, l’equilibrio fra tutte le forze orizzontali, le forze verticali e i momenti sul piano longitudinale, che si possono rappresentare in modo molto schematico nella Figura 4. Succede, però, che una causa perturbante, anche piccola, può modificare momentaneamente questo equilibrio.

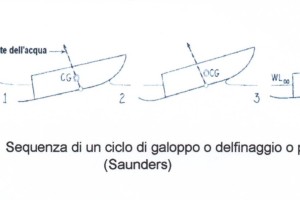
Se, per esempio, la risultante delle pressioni dinamiche agenti sul fondo passa alternativamente da una posizione a poppa a una posizione a prora del centro di gravità, lo scafo è soggetto a beccheggio, e questo beccheggio è associato con un “sali e scendi” che può sfociare in una serie di oscillazioni cicliche, che si mantengono automaticamente, e che gli americani chiamano “porpoising”. Noi potremmo dire con un termine che rispecchi bene il fenomeno, che lo scafo “galoppa” o “delfina”, cioè imita il modo di nuotare dei delfini, fenomeno che rappresenta per il progettista una vera e propria spina nel fianco.

Nella Figura 10 si vede la sequenza di un ciclo di “galoppo”. Se un’onda investe la prora, avremo un aumento della superficie bagnata di proravia e quindi uno spostamento in tal senso della pressione. La risultante delle pressioni dinamiche, quindi, si sposta a proravia del centro di gravità CG (condizione 1 della Figura 10). Subito dopo la prora si alza e il campo di pressioni si sposta verso poppa e la risultante passa per il centro di gravità CG (condizione 2 della Figura 10).

Se questa situazione si stabilizzasse non si verificherebbe alcun problema. Invece se la prora continua ad alzarsi, il campo di pressioni si sposta ancora di più verso poppa e la risultante passa a poppavia del centro di gravità CG (condizione 3 della Figura 10). In questa condizione si forma un momento appruante e quasi contemporaneamente l’onda perturbatrice passa sotto la poppa per cui la prora s’infila violentemente nell’acqua e la risultante delle pressioni passa a proravia del centro di gravità CG (condizione 4 della Figura 10). 

Da questo punto il ciclo del galoppo inizia da capo con sempre più energia. Il fenomeno può raggiungere effetti negativi al punto tale da poter creare notevoli danni alla struttura.

La resistenza totale al rimorchio di uno scafo planante ha quattro elementi fondamentali, cioè

La resistenza residua \(R_R\) , in cui è inclusa la resistenza di forma, di uno scafo planante, prima che questi raggiunga la velocità di planata, possiede le stesse caratteristiche generali della resistenza residua di un normale scafo dislocante e che molte di quelle caratteristiche di forma dello scafo che sono favorevoli al fenomeno della planata agiscono al contrario in senso negativo  sulla resistenza residua prima che detta planata avvenga.

Infatti

a) la larghezza, utile alla portanza, è nociva alla resistenza residua alle basse velocità;
b) la poppa larga, utile alla planata, è nociva alla resistenza residua perché causa turbolenza;
c) l’angolo di rialzo del fondo β ( Figura 11) che deve assumere valori piccoli per una buona planata e che al contrario dovrebbe essere aumentato nei riguardi della resistenza residua per conseguire forme di scafo snelle, oltre che per ottenere un buon comportamento in mare.

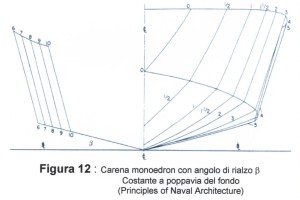
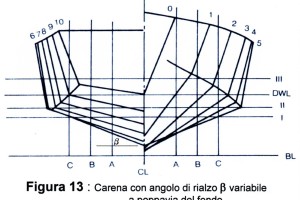
L’angolo di rialzo del fondo  β  è un valore molto importante poiché il suo modo di applicazione non solo definisce una carena monoedron, cioè con angolo costante a poppavia (Figura 12), o una carena con angolo di rialzo del fondo variabile (Figura 13), ma condiziona anche la resistenza e il comportamento in mare. Infatti, una carena con un angolo β  alto, in navigazione, penetra bene nell’acqua conseguendo accelerazioni minori.
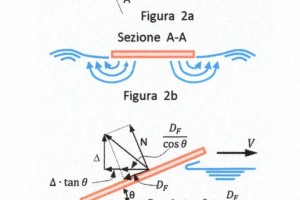
Come abbiamo già visto nella Figura 2 l’equazione che calcola la resistenza residua è

L’angolo di rialzo β e la lunghezza bagnata in chiglia quanto incidono sulla resistenza d’attrito? Argomento che sarà trattato nella prossima parte dell’articolo.

Angelo Sinisi