
La ricerca e lo sviluppo delle forme della carena - parte 6
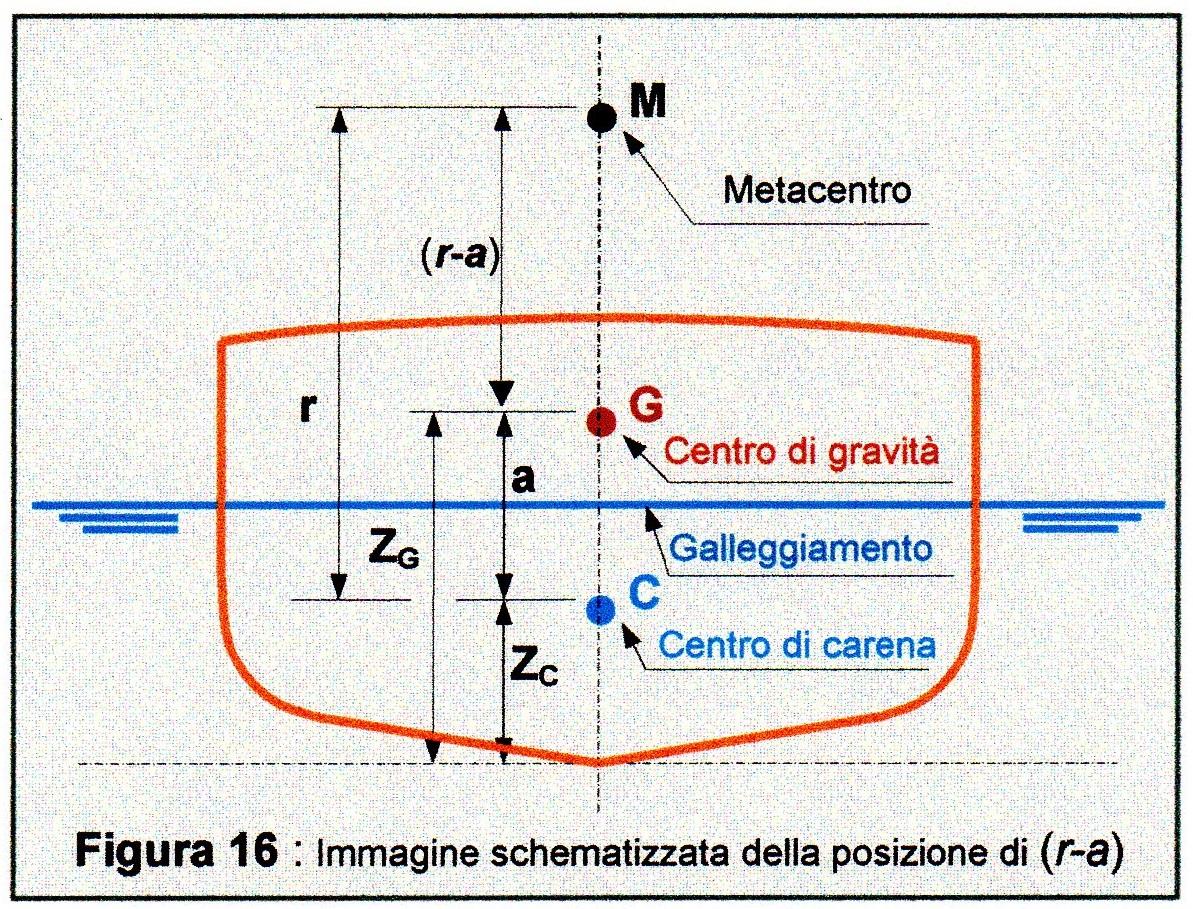
Un’altezza metacentrica elevata renderebbe fastidiosa la vita di bordo durante la navigazione. Ciò perché il periodo di oscillazione \(T_{t}\) della nave è inversamente proporzionale all’altezza metacentrica trasversale \((r-a)\) (Figura 16). Si deduce che un valore di \((r-a)\) elevato abbassa il periodo di oscillazione e di conseguenza aumenta la velocità angolare ωt con la relativa accelerazione e la nave acquista un comportamento “troppo duro” in mare ondoso.
Le notevoli accelerazioni angolari danno origine a grandi forze d’inerzia che possono provocare gravi danni alla nave e alle persone. Invece un’altezza metacentrica troppo bassa, se addolcisce il moto di oscillazione della nave, in mare molto mosso, può sempre costituire un pericolo per la nave fino al capovolgimento. Quindi l’altezza metacentrica trasversale è un valore determinante per la riuscita di un buon progetto, perché condiziona la larghezza al galleggiamento della nave. Infatti, il raggio metacentrico trasversale è determinato dal rapporto
\(r=\frac{J_{X} } {\nabla } \) |
|
\(J_X\) = momento d’inerzia trasversale della figura di galleggiamento |
|
|
\(\nabla\) = volume di carena |
Il volume di carena all’immersione \(T_i\) si può ottenere in due modi:
- integrando le aree trasversali all’immersione \(T_i\) per tutta la lunghezza nave da poppa a prora;
- integrando le aree delle figure di galleggiamento dall’immersione 0 fino all’immersione \(T_i\).
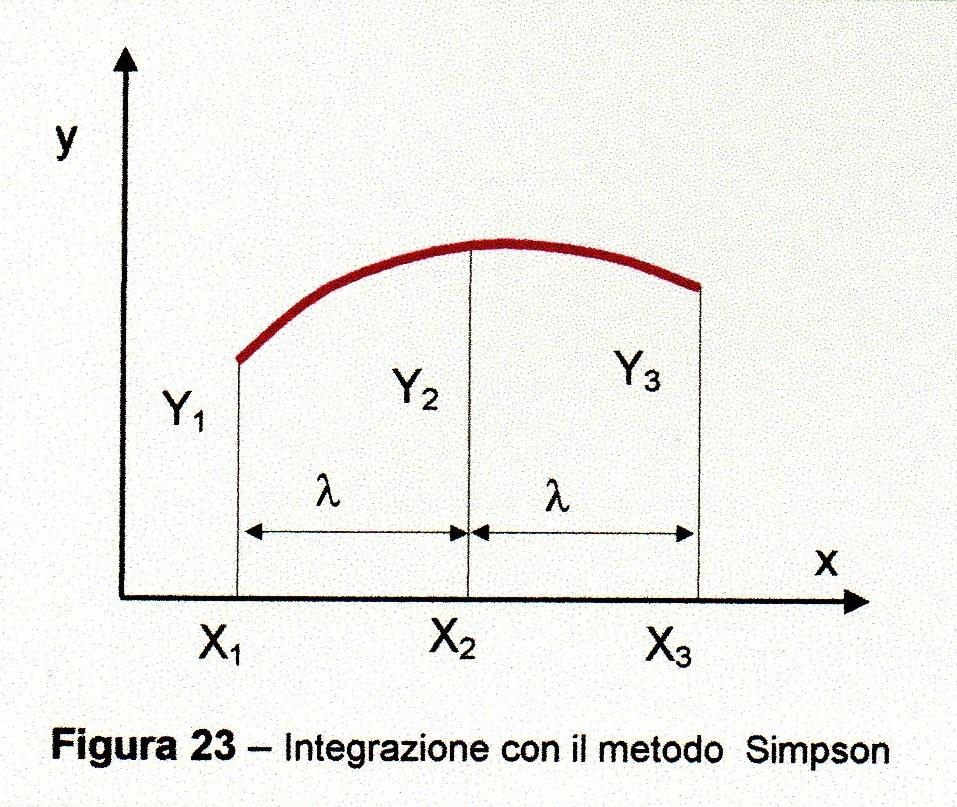
Per ottenere le aree delle sezioni trasversali o quelle dei galleggiamenti è preferibile usare il metodo di Simpson che da valori precisi perché utilizza una serie di curve paraboliche ogni due intervalli (Figura 23) di \(\lambda\), per cui:
\(A=\frac{2}{3}\cdot \lambda \cdot \sum_{0}^{n} (a\cdot y_i)\) |
|
\(\lambda\) = intervallo costante tra le semilarghezze della figura di galleggiamento alle varie ordinate o semilarghezze della sezione trasversale alle varie immer-sioni da integrare |
|
|
\(y_i\) = semilarghezze |
|
|
|
\(\sum_{0}^{n} (a\cdot y_i)\) = \((1 \cdot y_o+4 \cdot y_1 + 2 \cdot y_2 + 4 \cdot y_3 + ...............+4 \cdot y_{n-1}+1 \cdot y_n)\) |
|
|
|
\(n\) = numero delle ordinate o immersioni |
Il momento statico delle aree di galleggiamento o delle aree trasversali, rispettivamente riferite all’ordinata 0 o alla linea di costruzione L.C., è con il metodo Simpson
\(M_S=\frac{2}{3}\cdot \lambda^{2} \cdot \sum_{0}^{n} (a\cdot \beta \cdot y_i)\) |
|
\(\lambda\) = intervallo costante tra le semilarghezze della figura di galleggiamento alle varie ordinate o semilarghezze della sezione trasversale alle varie immersioni da integrare |
|
|
\(y_i\) = semilarghezze |
|
|
|
\(\beta\) = \(0,1,2,3......................(n-1),n\) |
|
|
|
\(\sum_{0}^{n} (a\cdot \beta \cdot y_i)\) = \((1 \cdot \beta \cdot y_o+4 \cdot \beta \cdot y_1 + 2 \cdot \beta \cdot y_2 + 4 \cdot \beta \cdot y_3 + ..........+4 \cdot \beta \cdot y_{n-1}+1 \cdot \beta \cdot y_n)\) |
|
|
|
\(n\) = numero delle ordinate o immersioni |
L’ascissa del centro dell’area di galleggiamento all’immersione \(T_i\) è data dal rapporto tra il momento statico della figura di galleggiamento riferito all’ordinata 0 e l’area della figura di galleggiamento, per cui si ha
\(X_{gi}= \frac{M_{S_i}}{A_i}\)
L’ascissa del centro di carena \(X_C\) relativa ad una immersione si ottiene dividendo il momento del volume rispetto all’ordinata 0 con il volume
\(X_{C}= \frac{M_{X_\nabla}}{\nabla}\)
Similmente l’ordinata del centro di carena \(Z_C\) relativa ad una immersione si ottiene dividendo il momento del volume rispetto alla L.C. con il relativo volume
\(Z_{C}= \frac{M_{Z_\nabla}}{\nabla}\)
Il momento d’inerzia longitudinale \(J_X\) della figura di galleggiamento all’immersione \(T_i\) si può trovare sia con il metodo di Simpson
\(J_X=\frac{2}{9}\cdot \lambda \cdot \sum_{0}^{n} (a\cdot y^{3}_i)\) |
|
\(\lambda\) =intervallo costante tra le semilarghezze \(y\) della figura di galleggiamento all’immersione \(T_i\) |
|
|
\(\sum_{0}^{n} (a\cdot y^{3}_i)\) = \((1 \cdot y_o^{3}+4 \cdot y_1^{3} + 2 \cdot y_2^{3} + 4 \cdot y_3^{3} + ...............+4 \cdot y_{n-1}^{3}+1 \cdot y_n^{3})\) |
|
|
|
\(n\) = numero delle semilarghezze |
Il momento d’inerzia longitudinale \(J_Y\) della figura di galleggiamento all’immersione \(T_i\) è
\(J_Y=\frac{2}{3}\cdot \lambda^3 \cdot \sum_{0}^{n} (a\cdot \beta^2 \cdot y_i)-A_i \cdot X_{g_i}^2\) |
|
\(\lambda\) =intervallo costante tra le semilarghezze \(y\) della figura di galleggiamento all’immersione \(T_i\) |
|
|
\(y_i\) = semilarghezze |
|
|
|
\(\beta\) = \(0,1,2,3,............(n-1),n\) |
|
|
|
\(\sum_{0}^{n} (a\cdot \beta^2 \cdot y_i)\) = \((1 \cdot \beta^2 \cdot y_o+4 \cdot \beta^2 \cdot y_1 + 2 \cdot \beta^2 \cdot y_2+ ....+4 \cdot \beta^2 \cdot y_{n-1}+1 \cdot \beta^2 \cdot y_n)\) |
|
|
|
\(n\) = numero delle semilarghezze |
|
|
|
\(A_i\) = area di galleggiamento relativa all’immersione \(T_i\) |
|
|
|
\(X_{g_i}\) = ascissa del centro dell’area di galleggiamento riferita all’ordinata zero relativa all’immersione \(T_i\) |
Rimane comunque la considerazione fondamentale che il progetto navale, a cominciare dalla scelta della carena e le primissime previsioni di potenza, non è soltanto uno studio rigorosamente matematico, determinato e definito, ma costituisce in realtà quanto di più libero e aperto possa desiderare una mente creativa.
LEGENDA
|
La nave è pur sempre un mezzo difficile da progettare, viaggia sul confine di due fluidi molto diversi per densità e viscosità cinematica, e sarà sempre il risultato di un grande compromesso. Pertanto la buona riuscita di un progetto è anche frutto d’intuizione e di arte. Si possono dare delle indicazioni, non stabilire regole.
In ciò, forse, sta il particolare interesse della materia.








