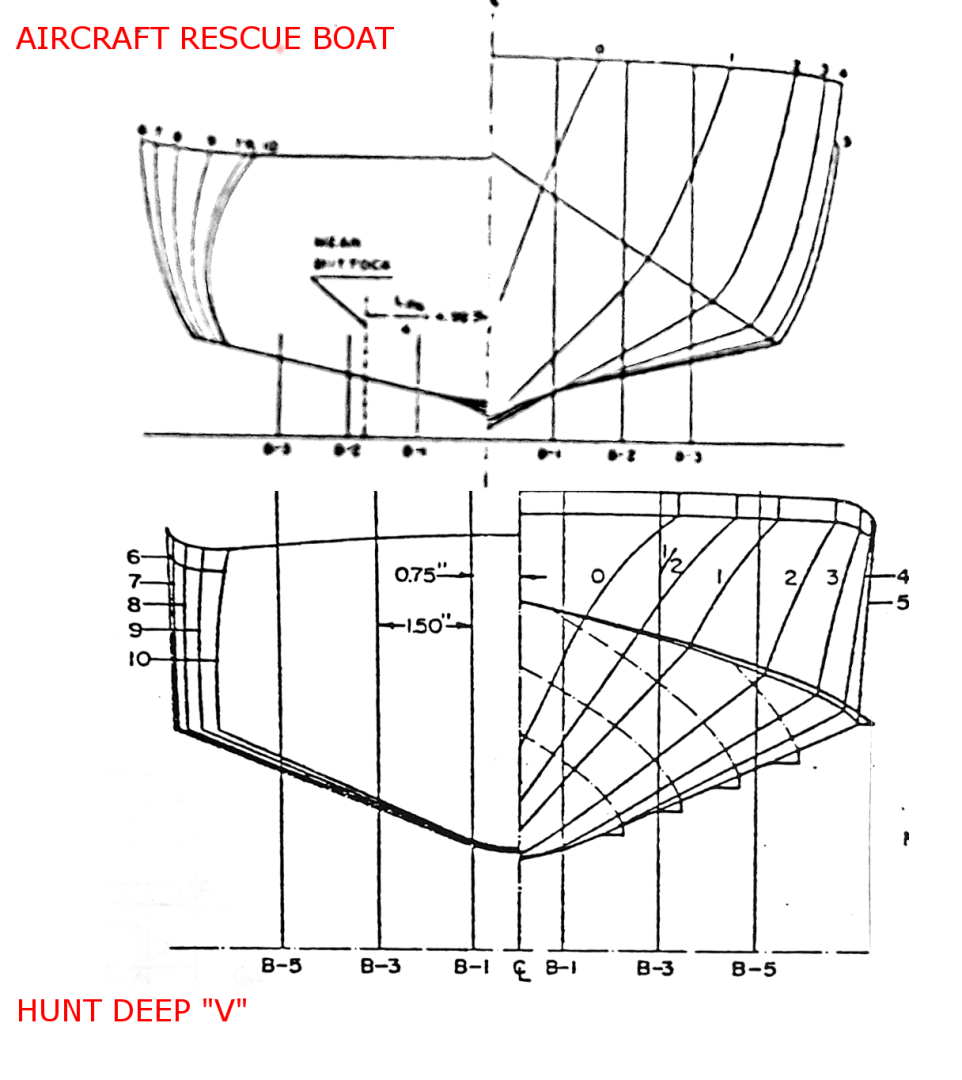
La ricerca e lo sviluppo delle forme della carena - parte 5
Nel progetto di una carena sono importanti non solo i calcoli idrodinamici per trovare il valore della potenza da installare, ma altrettanto lo sono i calcoli di statica, perché non solo definiscono i parametri per la stabilità, e quindi per la sicurezza, ma incidono anche sul comportamento in navigazione.
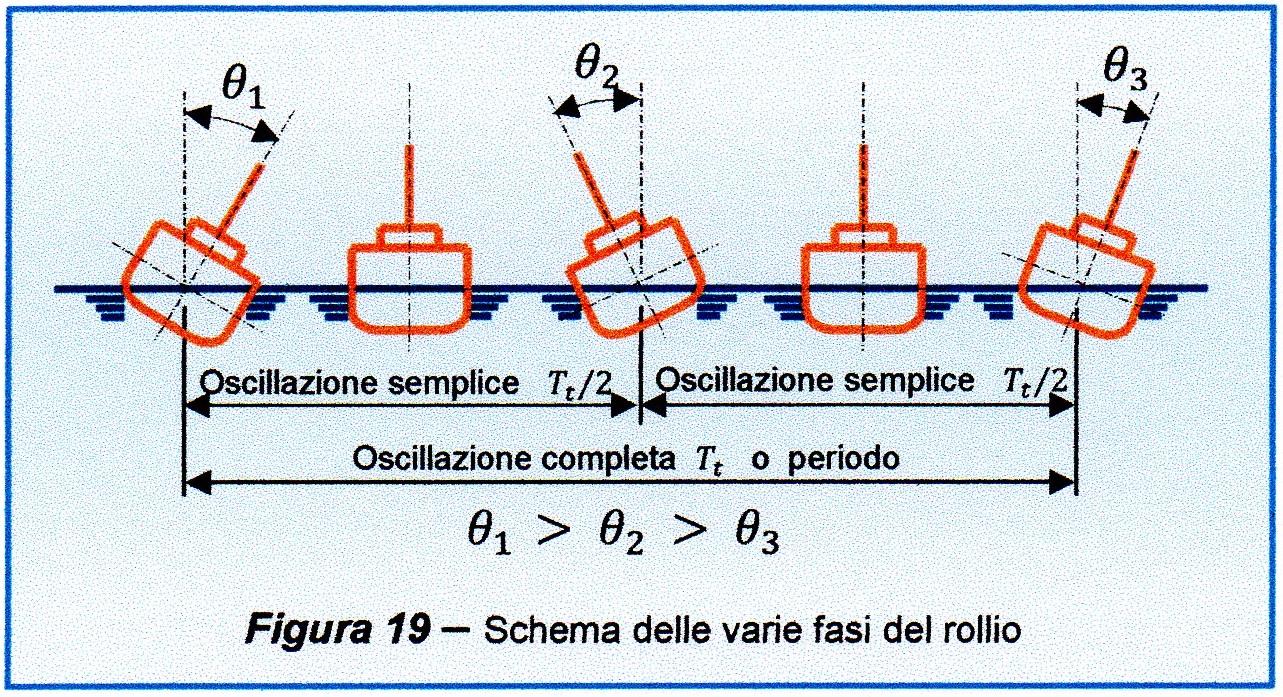
La durata dell’oscillazione completa trasversale, chiamato “periodo” di rollio (Figura 19), è rappresentata dalla relazione
\(T_{t}=2 \cdot π \cdot {\sqrt\frac{I_{YY} } {\Delta \cdot ( r - a ) } }\) |
|
\(I_{YY}=I_{t}+M_{{t}_{agg}}\) = momento d'inerzia di massa del sistema "nave-acqua" rispetto all'asse baricentrico longitudinale di rotazione |
|
|
\(I_{t}\) = momento d'inerzia di massa trasversale della nave rispetto all'asse baricentrico longitudinale di rotazione |
|
|
|
\(M_{{t}_{agg}}\) = "massa aggiunta" acqua di mare |
|
|
|
\(\Delta\) = dislocamento della nave |
|
|
|
\((r-a)\) = altezza metacentrica trasversale |
|
|
|
\(r\) = raggio metacentrico trasversale della figura di galleggiamento |
|
|
|
\(a\) = differenza tra l'ordinata del centro di gravità \(Z_{G}\) e l'ordinata del centro di carena \(Z_{C}\) |
|
|
|
\(π\) = rapporto tra la circonferenza e il diametro = 3,1415927 |
Se si indica con \(T_{t}\) la durata dell’oscillazione completa trasversale, cioè il periodo di rollio, con \(T_{t}/4\) si designa il tempo impiegato per passare dalla posizione diritta a quella di massima inclinazione (Figura 19).
La velocità angolare dopo un tempo t contato dal principio di ciascuna oscillazione è data da
\(ω_{t}=\theta \cdot {\frac{2 \cdot π}{T_{t}}} \cdot sin {\frac{2 \cdot π \cdot t }{T_{t}}}\) |
|
\(\theta\) = angolo massimo di rollio |
|
|
\(T_{t}\) = periodo di rollio |
Per ridurre la velocità angolare e conseguentemente l’accelerazione centrifuga conviene avere un periodo di oscillazione grande.
La formula del periodo di rollio \(T_{t}\) mostra che per ottenere ciò occorre aumentare il momento d’inerzia di massa \(I_{YY}\), oppure diminuire il valore dell’altezza metacentrica ( r - a ).
Certamente quest’ultimo provvedimento potrebbe non essere compatibile con la sicurezza di stabilità, soprattutto nelle navi piccole. Per questo il limite inferiore dell’altezza metacentrica, è legato alla stabilità della nave, è più alto per le navi piccole che quindi risultano più dure, cioè hanno un periodo di oscillazione piccolo e quindi accelerazioni (tangenziali e centrifughe) maggiori.
Quest’ultime possono essere tali da essere percepite in modo molto negativo dall’equipaggio e possono sollecitare le strutture dello scafo con forte intensità.
Il periodo di rollio \(T_{t}\) , in funzione dell’ampiezza dell’oscillazione \(\theta\), sarebbe costante se il raggio metacentrico trasversale, che il rapporto tra il momentod’inerzia trasversale della figura di galleggiamento ed il volume di carena, fosse costante al variare dello sbandamento.
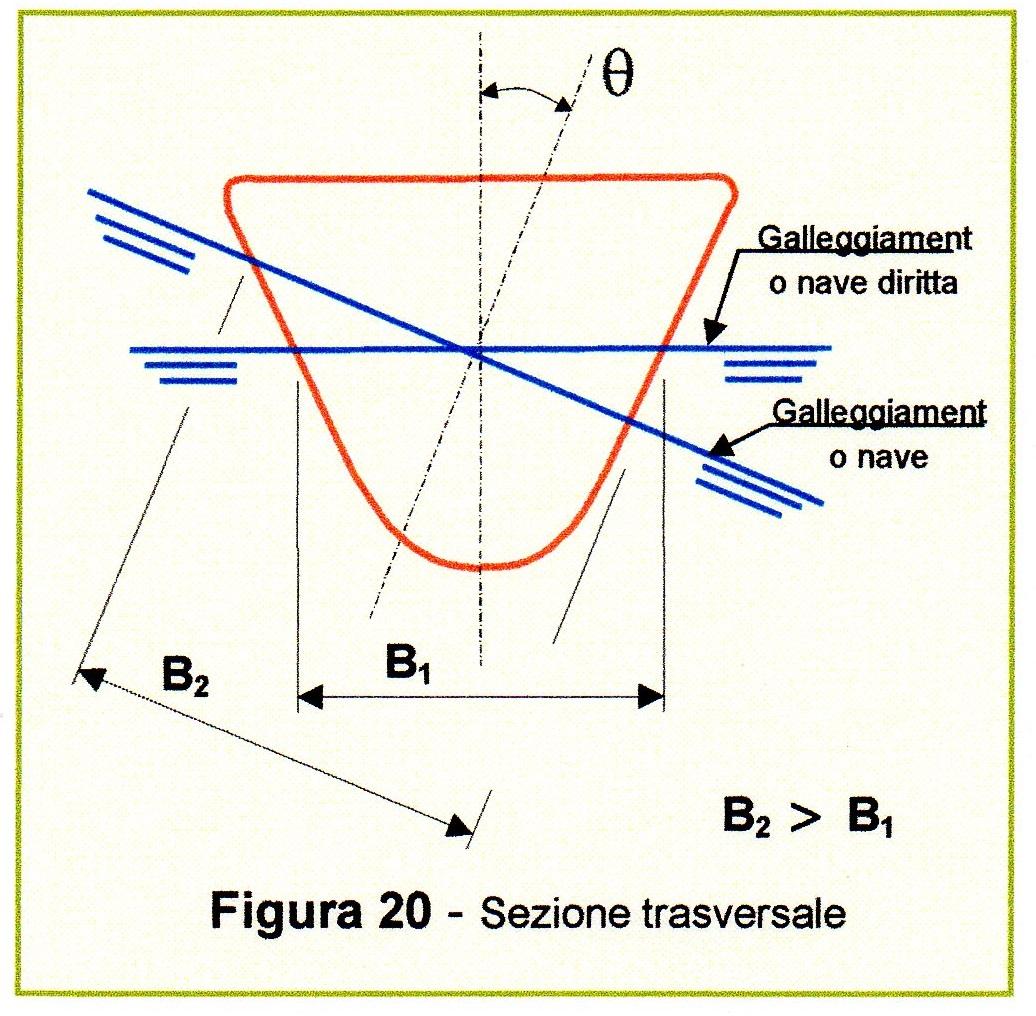
Invece, poiché la figura di galleggiamento varia per ampie oscillazioni (Figura 20), varia il momento d’inerzia trasversale e conseguentemente il raggio metacentrico trasversale, per cui varia il periodo di oscillazione.
Da quanto è stato detto, possiamo affermare che il rollio è un tipico fenomeno di “risonanza” e risulterà dalla combinazione delle azioni sbandanti e dalla “risposta” del sistema “nave-acqua”. Trattandosi di un fenomeno energetico, le capacità intrinseche del sistema di far “ritorno” alla condizione iniziale dipendono dalle caratteristiche “inerziali” del sistema stesso, che sono sostanzialmente legate alle forme di carena e alla distribuzione delle masse rispetto all’asse di rotazione.
Quindi sul rollio, cioè indirettamente sulla stabilità della nave, incide non solo la posizione verticale del baricentro, ma anche, in modo particolare, la distribuzione delle masse.
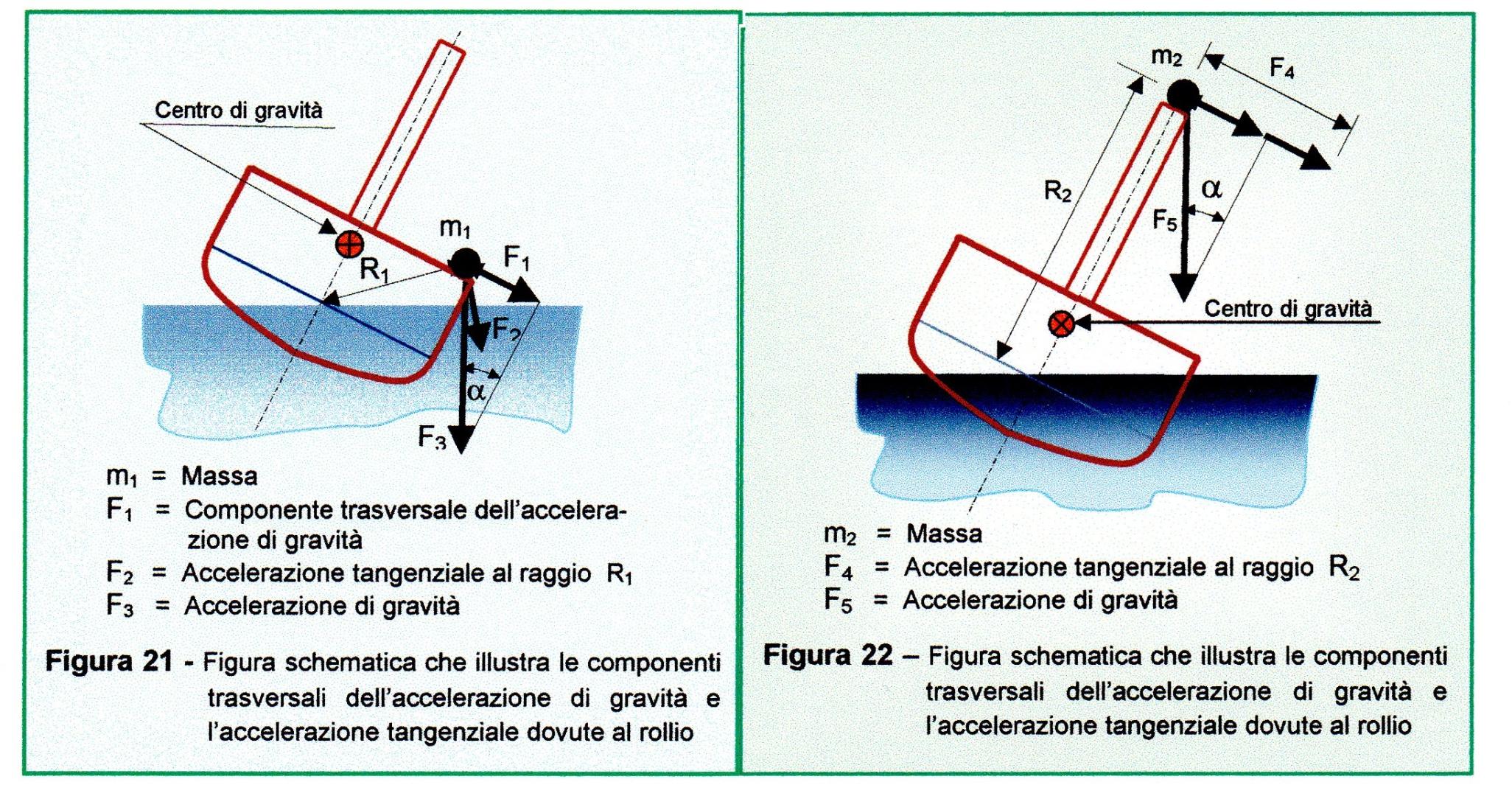
Le Figure 21 e 22 illustrano schematicamente come la stessa massa incida in modo diverso sulla forza trasversale secondo la sua posizione verticale, avendo la stessa posizione verticale e trasversale del centro di gravità. Infatti, due navi pur avendo lo stesso dislocamento \(\Delta\) e la stessa altezza metacentrica trasversale (r - a) potrebbero avere differente periodo di rollio \(T_{t}\) e la nave con il periodo maggiore potrebbe comportarsi come se avesse poca stabilità. Perciò due navi con momenti d’inerzia di massa differenti per avere lo stesso periodo di rollio devono necessariamente avere altezza metacentrica trasversale diverse.
\(T_{t}= 2 \cdot π \cdot {\sqrt\frac{I_{YY} } {\Delta \cdot ( r - a ) } } = 2 \cdot π \cdot {\sqrt\frac{{I}'_{YY} } {\Delta \cdot ( {r}' - {a}' ) } }\)
con uguali dislocamneti \(\Delta \) se \({I'}_{YY}>{I}_{YY}\) necessariamente sarà
\((r'-a')>(r-a)\)
|
|
|
||
a e a' = Differenza tra l’ordinata del centro di gravità \(Z_{G}\) e l’ordinata del centro di carena \(Z_{C}\) |
|
|||
\(I_{YY}=I_{t}+M_{{t}_{agg}}\)= Momento d’inerzia di massa del sistema "nave–acqua" rispetto all’asse baricentrico longitudinale di rotazione |
||||
\(I_{t}\)= Momento d’inerzia di massa trasversale della nave rispetto all’asse baricentrico longitudinale di rotazione |
|
|||
\(M_{{t}_{agg}}\) = "Massa aggiunta" di acqua di mare |
|
|||
\(\)r e r' = Raggio metacentrico trasversale della figura di galleggiamento = \(J_{X}/ \nabla\) |
|
|||
\((r-a)\) = Altezza metacentrica trasversale |
|
|||
\(T_{t}\) = Periodo di rollio |
\(=2 \cdot π \cdot {\sqrt\frac{I_{YY} } {\Delta \cdot ( r - a ) } }\) |
|
||
\(\Delta\)= Dislocamento della nave |
|
|||
\(\nabla\)= Volume di carena |
|
|||
\(π\)= Rapporto tra la circonferenza e il diametro = 3,1415927 |
|
|||
\(\theta\) = Angolo massimo di rollio |
|
|||
\(ω_t \) = Velocità angolare dopo un tempo |
\(t= \theta \cdot [(2\cdot π)/T_{t}] \cdot sin[(2 \cdot π \cdot t)/T_{t}]\) |
|
L’altezza metacentrica trasversale quanto incide su una navigazione confortevole di una nave? Nella prossima e ultima parte di questo articolo parleremo ancora dell’altezza metacentrica e conseguentemente del raggio metacentrico, degli elementi di statica e sistemi d’integrazione.
© Copyright All rights reserved








